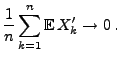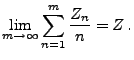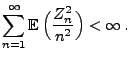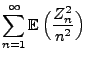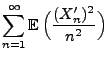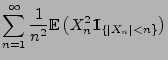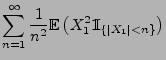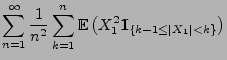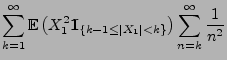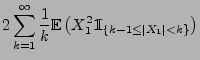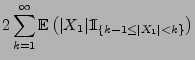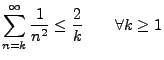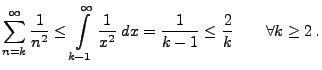Next: Anwendungsbeispiele
Up: Gesetz der großen Zahlen
Previous: Schwaches Gesetz der großen
Contents
Starkes Gesetz der großen Zahlen
- Wir diskutieren nun Bedingungen dafür, dass das in
(15) betrachtete arithmetische Mittel
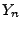 , nach
einer geeignet gewählten Zentrierung, fast sicher gegen Null
konvergiert, falls
, nach
einer geeignet gewählten Zentrierung, fast sicher gegen Null
konvergiert, falls
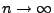 .
.
- In der Literatur nennt man Aussagen dieses Typs starkes
Gesetz der großen Zahlen.
- Eines der ersten Resultate in dieser Richtung ist das folgende
starke Gesetz der großen Zahlen, das auf Cantelli zurückgeht.
Theorem 5.14
Sei
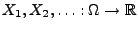
eine Folge von unabhängigen Zufallsvariablen mit
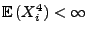
für alle
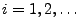
.
Falls es eine Konstante
gibt, so dass
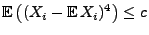 |
(17) |
für jedes
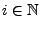
, dann gilt für
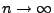
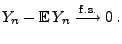 |
(18) |
- Beweis
-
- Ohne Einschränkung der Allgemeinheit können wir annehmen, dass
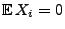 für alle
für alle
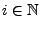 .
.
- Wegen Korollar 5.2 genügt es dann zu zeigen, dass
für jedes
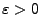
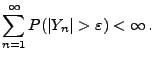 |
(19) |
- Aus der Markow-Ungleichung (4.73) für
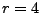 ergibt
sich, dass
ergibt
sich, dass
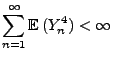 |
(20) |
hinreichend für die Gültigkeit von (19) ist.
- Wir zeigen nun, dass unter den getroffenen Voraussetzungen die
Bedingung (20) erfüllt ist.
- Es gilt
- Weil
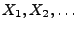 unabhängige Zufallsvariablen sind und weil
unabhängige Zufallsvariablen sind und weil
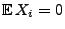 für alle
für alle
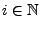 vorausgesetzt wird, ergibt sich
hieraus, dass
vorausgesetzt wird, ergibt sich
hieraus, dass
- Folglich gilt
- D.h., die Bedingung (20) ist erfüllt.

- Beachte
-
- Falls
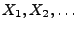 nicht nur unabhängige, sondern auch
identisch verteilte Zufallsvariablen sind, dann lassen sich die in
Theorem 5.14 formulierten
Integrierbarkeitsbedingungen deutlich abschwächen.
nicht nur unabhängige, sondern auch
identisch verteilte Zufallsvariablen sind, dann lassen sich die in
Theorem 5.14 formulierten
Integrierbarkeitsbedingungen deutlich abschwächen.
- Der ,,Preis'' hierfür ist allerdings, dass nun ein wesentlich
umfangreicherer Beweis erforderlich ist, im Vergleich zum Beweis
von Theorem 5.14.
- Dies führt zu der folgenden Version des starken Gesetzes der
großen Zahlen.
Theorem 5.15
Sei
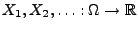
eine Folge von unabhängigen und identisch verteilten Zufallsvariablen
mit
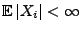
für alle
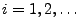
;
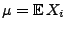
.
Dann gilt
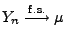
für
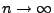
.
- Im Beweis von Theorem 5.15 benötigen wir
mehrere Hilfssätze, die auch von eigenständigem Interesse sind.
- Zunächst leiten wir eine einfache untere bzw. obere Schranke für
den Erwartungswert von nichtnegativen Zufallsvariablen her.
Lemma 5.1
Sei
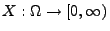
eine nichtnegative Zufallsvariable mit
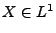
, d.h.
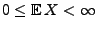
. Dann gilt
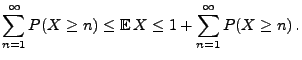 |
(21) |
- Beweis
 Es gilt
Es gilt

Ein weiteres nützliches Hilfsmittel ist die folgende Ungleichung von Kolmogorow.
Lemma 5.2
(Kolmogorow)
Seien
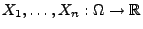
unabhängige Zufallsvariablen
mit
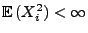
und
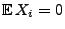
für jedes
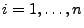
.
Für jedes
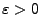
und
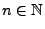
gilt dann
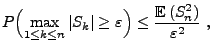 |
(22) |
wobei
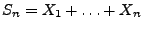
.
- Beweis
-
- Sei
und für
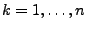
- Dann gilt
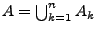 und folglich
und folglich
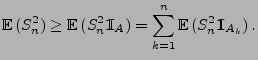 |
(23) |
- Weil
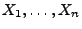 unabhängige Zufallsvariablen sind, sind
wegen Theorem 3.18 auch
unabhängige Zufallsvariablen sind, sind
wegen Theorem 3.18 auch
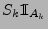 und
und
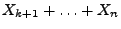 unabhängige Zufallsvariablen.
unabhängige Zufallsvariablen.
- Aus der Multiplikationsformel für den Erwartungswert des Produktes
von unabhängigen Zufallsvariablen (vgl. Theorem 4.9)
ergibt sich deshalb, dass
- Hieraus ergibt sich, dass
- Mit Hilfe von (23) ergibt dies, dass

Außerdem benötigen wir den folgenden Hilfssatz.
Lemma 5.3
Seien
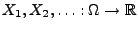
unabhängige Zufallsvariablen
mit
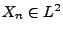
und
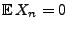
für alle
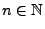
. Falls
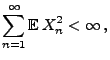 |
(24) |
dann gibt es eine Zufallsvariable
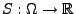
, so dass
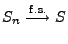
, wobei
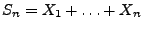
.
- Beweis
-
Die nächsten beiden Hilfssätze betreffen zwei klassische
Konvergenzeigenschaften von Folgen reller Zahlen. Sie werden in
der Literatur Lemma von Toeplitz bzw. Lemma von
Kronecker genannt.
Lemma 5.4
(Toeplitz) Seien
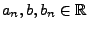
relle Zahlen mit
 und und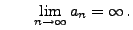 |
(26) |
Falls
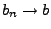
, dann gilt
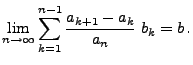 |
(27) |
- Beweis
-
Lemma 5.5
(Kronecker) Seien
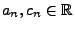
relle Zahlen, so dass die Bedingung
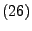
erfüllt ist. Falls die Reihe
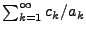
konvergiert, dann gilt
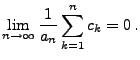 |
(29) |
- Beweis
-
- Beweis von Theorem 5.15
-
- Die Behauptung gilt genau dann, wenn
mit Wahrscheinlichkeit 1.
- Ohne Einschränkung der Allgemeinheit setzen wir voraus, dass
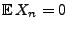 und zeigen, dass
und zeigen, dass
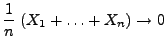 |
(31) |
mit Wahrscheinlichkeit 1.
- Aus Lemma 5.1 ergibt sich, dass
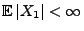 genau dann, wenn
genau dann, wenn
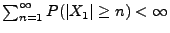 .
.
- Weil
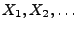 identisch verteilt sind, gilt dies genau
dann, wenn
identisch verteilt sind, gilt dies genau
dann, wenn
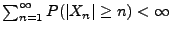 .
.
- Wegen des Lemmas von Borel-Cantelli (vgl.
Korollar 2.3 und Theorem 2.7)
ist das gleichbedeutend mit
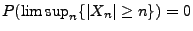 .
.
- Hieraus folgt, dass es für fast jedes
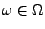 eine
natürliche Zahl
eine
natürliche Zahl
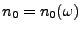 gibt, so dass
gibt, so dass
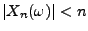 für jedes
für jedes 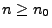 gilt.
gilt.
- Also gilt (31) genau dann, wenn
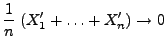 |
(32) |
mit Wahrscheinlichkeit 1, wobei für
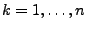
- Beachte: Der Übergang von
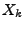 zu
zu
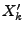 wird Abschneidetechnik genannt.
wird Abschneidetechnik genannt.
- Weil
ergibt sich aus Lemma 5.4 mit
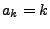 , dass
, dass
- Deshalb gilt (32) und damit auch
(31) genau dann, wenn
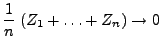 |
(33) |
mit Wahrscheinlichkeit 1, wobei
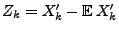 .
.
- Aus Lemma 5.5 mit
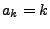 und
und
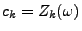 ergibt sich die Gültigkeit von (33), wenn gezeigt
wird, dass es eine Zufallsvariable
ergibt sich die Gültigkeit von (33), wenn gezeigt
wird, dass es eine Zufallsvariable 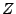 gibt, so dass mit
Wahrscheinlichkeit 1
gibt, so dass mit
Wahrscheinlichkeit 1
- Wegen Lemma 5.3 genügt es nun zu zeigen, dass
- Dies ergibt sich aus den folgenden Abschätzungen:
wobei in der vorletzten Abschätzung die Ungleichung
verwendet wurde, die sich ergibt aus
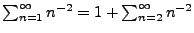 und
und
- Damit ist Theorem 5.15 bewiesen.





Next: Anwendungsbeispiele
Up: Gesetz der großen Zahlen
Previous: Schwaches Gesetz der großen
Contents
Ursa Pantle
2004-05-10
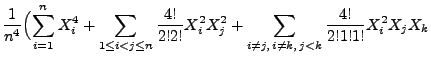
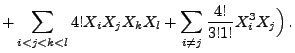
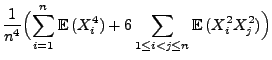
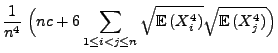
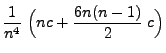
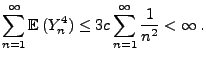
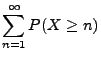
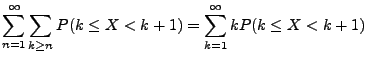
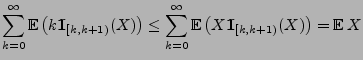
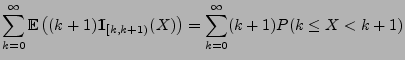
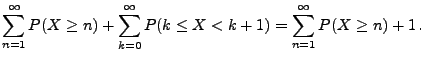
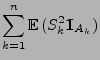
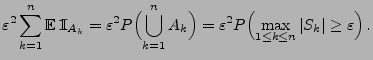
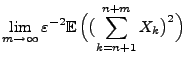
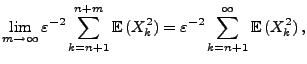
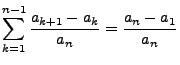
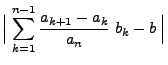
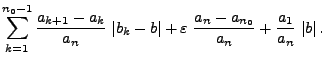
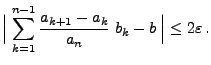
![$\displaystyle X_k^\prime=\left\{\begin{array}{ll} X_k\,, & \mbox{falls $\vert X...
...
k$,}\\ [3\jot]
0\,, & \mbox{falls $\vert X_k\vert\ge k$.}
\end{array}\right.
$](img1892.png)