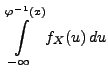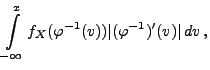Ein wichtiger Spezialfall einer zusammengesetzten Abbildung ist
die lineare Transformation von Zufallsvariablen, wobei 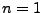 und
und
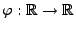 mit
mit
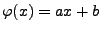 ;
;
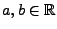 .
.
Theorem 3.13
Sei
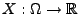
eine beliebige Zufallsvariable und
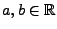
beliebige Zahlen mit
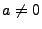
. Dann ist
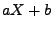
eine Zufallsvariable,
und
- 1.
- die Verteilungsfunktion von
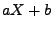 ist
gegeben durch
ist
gegeben durch
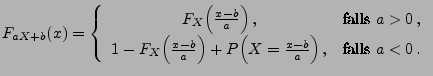 |
(37) |
- 2.
- falls
 absolutstetig ist mit der Dichte
absolutstetig ist mit der Dichte 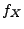 , dann ist auch
, dann ist auch
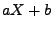 absolutstetig mit der Dichte
absolutstetig mit der Dichte
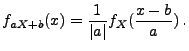 |
(38) |
![]() und
und
![]() mit
mit
![]() ;
;
![]() .
.