



Next: Jensen-Ungleichung
Up: Ungleichungen für Momente und
Previous: Ungleichungen für Momente und
Contents
Ungleichungen vom 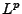 -Typ
-Typ
- In diesem Abschnitt verallgemeinern wir die Ungleichung (48)
von Cauchy-Schwarz und leiten weitere Ungleichungen dieses Typs
her, die wir Ungleichungen vom
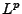 -Typ nennen.
-Typ nennen.
- Dabei ist das folgende Hilfsergebnis nützlich, das manchmal die
Ungleichung von Young genannt wird.
Lemma 4.3
Sei
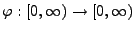
eine stetige und streng
monoton wachsende Funktion mit
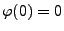
und
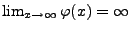
. Für die Funktionen
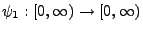
und
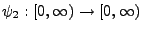
mit
gilt dann
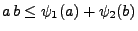 |
(63) |
für beliebige
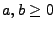
, wobei
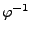
die zu
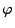
inverse Funktion ist.
- Beweis
-
- Definition
-
- Sei
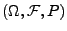 ein beliebiger Wahrscheinlichkeitsraum, und
sei
ein beliebiger Wahrscheinlichkeitsraum, und
sei
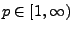 eine beliebige Zahl.
eine beliebige Zahl.
- Mit
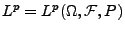 bezeichnen wir dann die Familie
aller Zufallsvariablen
bezeichnen wir dann die Familie
aller Zufallsvariablen
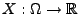 , für die
, für die
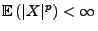 .
.
- Für jedes
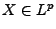 heißt
heißt
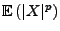 das
das 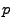 -te absolute
Moment von
-te absolute
Moment von  .
.
Wir leiten nun eine Abschätzung für das (erste) absolute Moment
des Produktes zweier Zufallsvariablen her.
Theorem 4.15
(Hölder-Ungleichung)

Sei
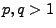
, so dass
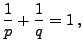 |
(64) |
und seien
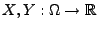
beliebige Zufallsvariablen mit
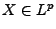
und
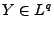
. Dann gilt
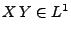
und
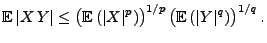 |
(65) |
- Beweis
-
- Beachte
-
- Als Spezialfall der Ungleichung (65) von Hölder
ergibt sich für
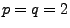 die Ungleichung (48) von
Cauchy-Schwarz.
die Ungleichung (48) von
Cauchy-Schwarz.
- Eine weitere Folgerung aus der Ungleichung (65) von Hölder
ist das folgende Resultat.
Korollar 4.6
(Ljapunow-Ungleichung)

Falls
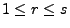
, dann gilt
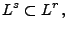 |
(66) |
und für jedes
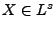
gilt
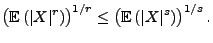 |
(67) |
- Beweis
-
Es gilt die folgende Abschätzung für das 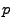 -te absolute Moment
der Summe von zwei Zufallvariablen.
-te absolute Moment
der Summe von zwei Zufallvariablen.
Theorem 4.16
(Minkowski-Ungleichung)

Falls
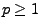
und
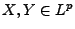
, dann gilt
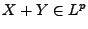
und
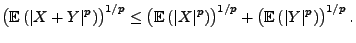 |
(68) |
- Beweis
-




Next: Jensen-Ungleichung
Up: Ungleichungen für Momente und
Previous: Ungleichungen für Momente und
Contents
Ursa Pantle
2004-05-10
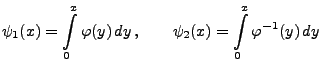
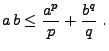
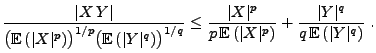
![]() -te absolute Moment
der Summe von zwei Zufallvariablen.
-te absolute Moment
der Summe von zwei Zufallvariablen.