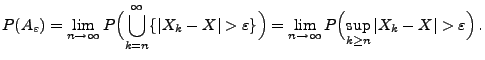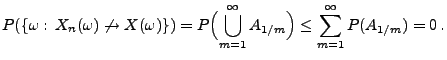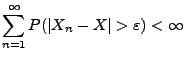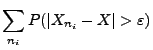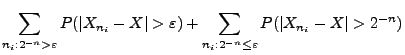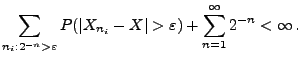Next: Charakterisierung der Verteilungskonvergenz
Up: Konvergenzarten
Previous: Konvergenzarten
Contents
Definitionen und
elementare Eigenschaften
- Definition
 Seien
Seien
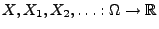 beliebige Zufallsvariablen. Man sagt: Die Folge
beliebige Zufallsvariablen. Man sagt: Die Folge
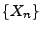 konvergiert fast sicher gegen
konvergiert fast sicher gegen  , falls
, falls
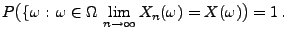 |
(1) |
Schreibweise:
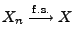
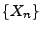 konvergiert in Wahrscheinlichkeit gegen
konvergiert in Wahrscheinlichkeit gegen  , falls
für jedes
, falls
für jedes
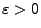
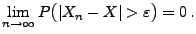 |
(2) |
Schreibweise:
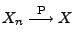
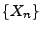 konvergiert im
konvergiert im 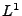 gegen
gegen  , falls
, falls
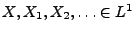 und
und
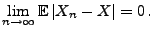 |
(3) |
Schreibweise:
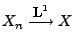
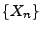 konvergiert im quadratischen Mittel gegen
konvergiert im quadratischen Mittel gegen  ,
falls
,
falls
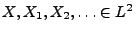 und
und
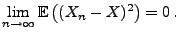 |
(4) |
Schreibweise:
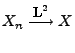
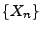 konvergiert in Verteilung gegen
konvergiert in Verteilung gegen  , falls
, falls
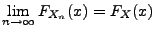 |
(5) |
für jeden Stetigkeitspunkt
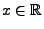 der Verteilungsfunktion
der Verteilungsfunktion
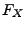 .
.
Schreibweise:
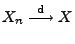
- Beachte
-
- Falls
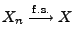 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 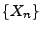 mit Wahrscheinlichkeit 1 gegen
mit Wahrscheinlichkeit 1 gegen  konvergiert.
konvergiert.
- Falls
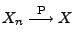 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 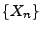 stochastisch gegen
stochastisch gegen  konvergiert.
konvergiert.
- Falls
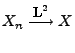 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 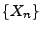 im
im
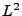 gegen
gegen  konvergiert.
konvergiert.
Das folgende Konvergenzkriterium ist ein nützliches
Hilfsmittel beim Beweis tieferliegender Grenzwertsätze.
- Beweis
-
Aus Theorem 5.1 ergibt sich sofort, dass die fast
sichere Konvergenz stets die Konvergenz in Wahrscheinlichkeit
impliziert.
- Beweis
 In Theorem 5.1 wurde gezeigt, dass
In Theorem 5.1 wurde gezeigt, dass
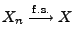 die
Gültigkeit von
die
Gültigkeit von
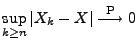 und damit auch
und damit auch
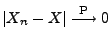 impliziert. Dies ist aber gleichbedeutend mit
impliziert. Dies ist aber gleichbedeutend mit
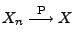 .
.

Außerdem gibt es die folgende hinreichende Bedingung für die fast
sichere Konvergenz.
- Beweis
-
- Aus (8) und aus dem Lemma von Borel-Cantelli (vgl.
Korollar 2.3) ergibt sich, dass
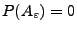 für jedes
für jedes
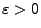 ,
,
- wobei
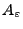 die in (7) eingeführte Menge
ist.
die in (7) eingeführte Menge
ist.
- Die Behauptung ergibt sich nun genauso wie im zweiten Teil des
Beweises von Theorem 5.1.

- Beachte
-
- Es gilt also
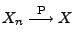 genau dann, wenn die Wahrscheinlichkeiten
genau dann, wenn die Wahrscheinlichkeiten
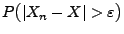 für jedes
für jedes
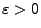 gegen
Null konvergieren.
gegen
Null konvergieren.
- Im Unterschied hierzu gilt
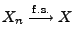 , wenn (jedoch nicht nur
dann) diese Null-Konvergenz hinreichend schnell erfolgt, so dass
die Summe in (8) endlich ist.
, wenn (jedoch nicht nur
dann) diese Null-Konvergenz hinreichend schnell erfolgt, so dass
die Summe in (8) endlich ist.
Eine andere Charakterisierung der Konvergenz in Wahrscheinlichkeit
lässt sich durch die Betrachtung von Teilfolgen gewinnen.
Theorem 5.2
Es gilt
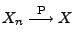
genau dann, wenn es für jede Teilfolge
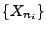
von
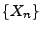
eine Teilfolge
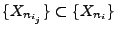
gibt, so dass
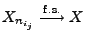
.
- Beweis
-
Wir zeigen nun, dass ebenfalls die L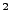 -Konvergenz und die
L
-Konvergenz und die
L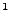 -Konvergenz stets die Konvergenz in Wahrscheinlichkeit
implizieren.
-Konvergenz stets die Konvergenz in Wahrscheinlichkeit
implizieren.
- Beweis

- Beweis

Als nächstes zeigen wir, dass die Konvergenz in Wahrscheinlichkeit
stets die Konvergenz in Verteilung impliziert.
- Beweis

- Es gelte
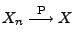 , d.h.,
, d.h.,
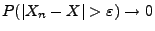 für
jedes
für
jedes
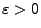 .
.
- Für beliebige
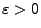 und
und
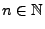 gilt
gilt
- Hieraus und wegen
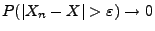 ergibt sich nun,
dass
ergibt sich nun,
dass
- Weil
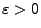 beliebig klein gewählt werden kann und weil
die Verteilungsfunktion
beliebig klein gewählt werden kann und weil
die Verteilungsfunktion 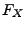 rechtsseitig stetig ist, ergibt sich
somit, dass für jedes
rechtsseitig stetig ist, ergibt sich
somit, dass für jedes
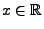
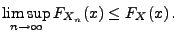 |
(9) |
- Sei nun
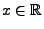 ein Stetigkeitspunkt der Verteilungsfunktion
ein Stetigkeitspunkt der Verteilungsfunktion
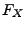 , d.h., es gelte
, d.h., es gelte
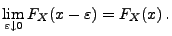 |
(10) |
- Ähnlich wie im ersten Teil des Beweises ergibt sich für beliebige
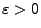 und
und
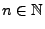 , dass
, dass
- Mit Hilfe von (10) ergibt sich somit, dass
- Hieraus und aus (9) folgt, dass
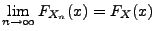 .
.

- Beachte
-
- Die Umkehrung der Aussage von Theorem 5.5 gilt im
allgemeinen nicht.
- Falls jedoch die ,,Grenzzufallsvariable''
 mit
Wahrscheinlichkeit
mit
Wahrscheinlichkeit 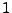 einunddenselben (deterministischen)
Wert annimmt, dann gilt auch die folgende umgekehrte Aussage.
einunddenselben (deterministischen)
Wert annimmt, dann gilt auch die folgende umgekehrte Aussage.
- Beweis





Next: Charakterisierung der Verteilungskonvergenz
Up: Konvergenzarten
Previous: Konvergenzarten
Contents
Ursa Pantle
2004-05-10
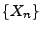 konvergiert fast sicher gegen
konvergiert fast sicher gegen  , falls
, falls
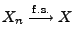
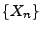 konvergiert in Wahrscheinlichkeit gegen
konvergiert in Wahrscheinlichkeit gegen  , falls
für jedes
, falls
für jedes
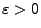
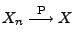
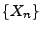 konvergiert im
konvergiert im 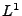 gegen
gegen  , falls
, falls
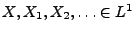 und
und
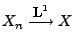
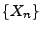 konvergiert im quadratischen Mittel gegen
konvergiert im quadratischen Mittel gegen  ,
falls
,
falls
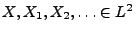 und
und
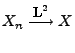
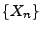 konvergiert in Verteilung gegen
konvergiert in Verteilung gegen  , falls
, falls
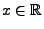 der Verteilungsfunktion
der Verteilungsfunktion
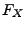 .
.
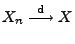
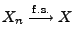 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 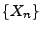 mit Wahrscheinlichkeit 1 gegen
mit Wahrscheinlichkeit 1 gegen  konvergiert.
konvergiert.
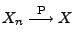 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 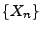 stochastisch gegen
stochastisch gegen  konvergiert.
konvergiert.
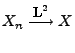 , dann sagt man auch, dass die Folge
, dann sagt man auch, dass die Folge 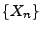 im
im
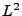 gegen
gegen  konvergiert.
konvergiert.