



Nächste Seite: Lineare und quadratische Formen
Aufwärts: Multivariate Normalverteilung
Vorherige Seite: Lineare Transformation von normalverteilten
Inhalt
Singuläre multivariate Normalverteilung
Der in Abschnitt 1.2.1
eingeführten Begriff der (regulären)
multivariaten Normalverteilung lässt sich wie folgt
verallgemeinern.
- Definition
-
- Sei
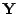 ein
ein  -dimensionaler Zufallsvektor mit
Erwartungswertvektor
-dimensionaler Zufallsvektor mit
Erwartungswertvektor
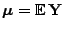 und Kovarianzmatrix
und Kovarianzmatrix
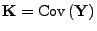 , so dass
, so dass
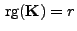 mit
mit 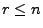 .
.
- Dann heißt
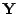 normalverteilt, wenn
normalverteilt, wenn
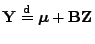 , wobei
, wobei
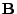 eine
eine 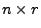 Matrix mit
Matrix mit
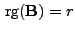 ist, die der Gleichung (24) genügt,
und
ist, die der Gleichung (24) genügt,
und
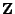 ein
ein 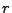 -dimensionaler Zufallsvektor mit
-dimensionaler Zufallsvektor mit
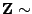 N
N
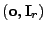 ist.
ist.
- Wir sagen, dass
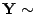 N
N
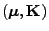 singulär
normalverteilt ist, wenn
singulär
normalverteilt ist, wenn
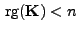 .
.
(Schreibweise:
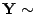 N
N
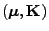 )
)
- Beachte
-
- Wenn
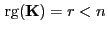 , dann ist der Zufallsvektor
, dann ist der Zufallsvektor
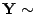 N
N
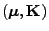 nicht absolutstetig,
nicht absolutstetig,
- denn die Werte von
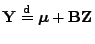 liegen mit
Wahrscheinlichkeit
liegen mit
Wahrscheinlichkeit 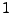 in der
in der 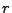 -dimensionalen Teilmenge
-dimensionalen Teilmenge
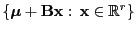 des
des
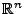 ,
,
- d.h., die Verteilung von
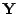 besitzt keine Dichte bezüglich
des
besitzt keine Dichte bezüglich
des  -dimensionalen Lebesgue-Maßes.
-dimensionalen Lebesgue-Maßes.
- Ein Beispiel hierfür ist der Zufallsvektor
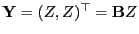 mit
mit
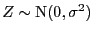 und
und
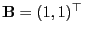 , der nur
Werte auf der Diagonalen
, der nur
Werte auf der Diagonalen
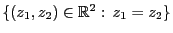 annimmt.
annimmt.
- Die Verteilung des Zufallsvektors
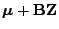 hängt nicht von der Wahl der Matrix
hängt nicht von der Wahl der Matrix
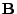 in der
Faktorisierungsgleichung (24) ab.
in der
Faktorisierungsgleichung (24) ab.
- Dies ergibt sich unmittelbar aus den folgenden beiden Kriterien
für das Vorliegen von (singulären bzw. regulären) multivariaten
Normalverteilungen.
Der Beweis von Theorem 1.4 wird in den Übungen
diskutiert (vgl. Übungsaufgabe 2.2). Er wird deshalb hier
weggelassen.




Nächste Seite: Lineare und quadratische Formen
Aufwärts: Multivariate Normalverteilung
Vorherige Seite: Lineare Transformation von normalverteilten
Inhalt
Hendrik Schmidt
2006-02-27