



Nächste Seite: Singuläre multivariate Normalverteilung
Aufwärts: Multivariate Normalverteilung
Vorherige Seite: Randverteilungen und Unabhängigkeit von
Inhalt
Lineare Transformation von normalverteilten
Zufallsvektoren
Wir zeigen nun, dass die Lineartransformation normalverteilter
Zufallsvektoren erneut zu normalverteilten Zufallsvektoren führt.
- Beweis
-
Aus Theorem 1.3 ergibt sich insbesondere, dass sich
normalverteilte Zufallsvektoren durch Lineartransformation von
Vektoren konstruieren lassen, deren Komponenten unabhängige und
N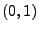 -verteilte Zufallsvariablen sind.
-verteilte Zufallsvariablen sind.
Korollar 1.5
- Seien
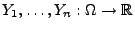 unabhängige
Zufallsvariablen mit
unabhängige
Zufallsvariablen mit
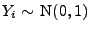 für jedes
für jedes
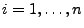 , d.h.
, d.h.
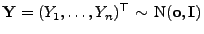 .
.
- Sei
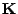 eine symmetrische und positiv definite
eine symmetrische und positiv definite 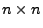 Matrix, und sei
Matrix, und sei
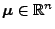 .
.
- Für den Zufallsvektor
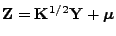 gilt dann
gilt dann
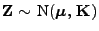 , wobei
, wobei
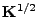 die
Quadratwurzel von
die
Quadratwurzel von
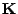 ist.
ist.
- Beweis
-
- Aus Theorem 1.3 ergibt sich, dass
- Hieraus und aus Lemma 1.6 folgt die Behauptung.





Nächste Seite: Singuläre multivariate Normalverteilung
Aufwärts: Multivariate Normalverteilung
Vorherige Seite: Randverteilungen und Unabhängigkeit von
Inhalt
Hendrik Schmidt
2006-02-27
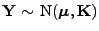 ein
ein  -dimensionaler
normalverteilter Zufallsvektor mit Erwartungswertvektor
-dimensionaler
normalverteilter Zufallsvektor mit Erwartungswertvektor
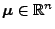 und mit (positiv definiter) Kovarianzmatrix
und mit (positiv definiter) Kovarianzmatrix
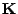 .
.
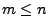 , und
, und
 sei eine beliebige
sei eine beliebige 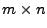 Matrix mit vollem Rang
Matrix mit vollem Rang
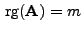 bzw.
bzw.
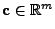 ein
beliebiger
ein
beliebiger 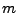 -dimensionaler Vektor.
-dimensionaler Vektor.
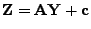 ein (
ein (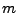 -dimensionaler)
normalverteilter Zufallsvektor mit
-dimensionaler)
normalverteilter Zufallsvektor mit