



Nächste Seite: Normalengleichung
Aufwärts: Lineare Modelle; Designmatrix mit
Vorherige Seite: Lineare Modelle; Designmatrix mit
Inhalt
Methode der kleinsten Quadrate
Das Ziel dieses Abschnittes besteht darin, die unbekannten
Modellparameter
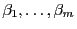 und
und 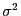 aus den
beobachteten Daten
aus den
beobachteten Daten
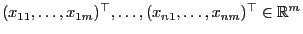 und
und
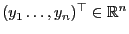 zu schätzen.
zu schätzen.
- Beachte
 Außer den in (5) gemachten
Modellannahmen werden zunächst keine zusätzlichen Voraussetzungen
über die Verteilung der zufälligen Störgrößen
Außer den in (5) gemachten
Modellannahmen werden zunächst keine zusätzlichen Voraussetzungen
über die Verteilung der zufälligen Störgrößen
 benötigt.
benötigt.
Unterabschnitte
Hendrik Schmidt
2006-02-27
![]() und
und ![]() aus den
beobachteten Daten
aus den
beobachteten Daten
![]() und
und
![]() zu schätzen.
zu schätzen.