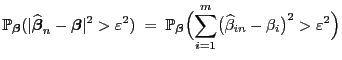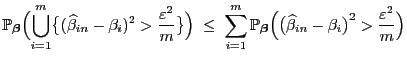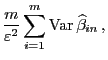Nächste Seite: Erwartungstreue Schätzung der Varianz
Aufwärts: Methode der kleinsten Quadrate
Vorherige Seite: Normalengleichung
Inhalt
Güteeigenschaften des KQ-Schätzers
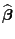
Wir setzen von jetzt an in Abschnitt 2.1 stets
voraus, dass die Designmatrix
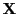 vollen (Spalten-) Rang hat
und leiten drei verschiedene Güteeigenschaften des in
(10) gegebenen KQ-Schätzers
vollen (Spalten-) Rang hat
und leiten drei verschiedene Güteeigenschaften des in
(10) gegebenen KQ-Schätzers
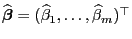 her.
her.
Theorem 2.2

Der Schätzer
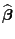
ist erwartungstreu für

, d.h., es gilt
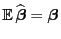
für jedes
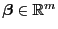
.
- Beweis
 Wegen
Wegen
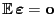 ergibt sich aus (6) und
(10), dass
ergibt sich aus (6) und
(10), dass

Der KQ-Schätzer
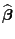 besitzt außerdem die
folgende Eigenschaft der Varianzminimalität. Dabei bezeichne
besitzt außerdem die
folgende Eigenschaft der Varianzminimalität. Dabei bezeichne
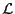 die Familie aller erwartungstreuen linearen Schätzer
die Familie aller erwartungstreuen linearen Schätzer
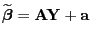 für
für
 , wobei
, wobei
 eine
eine
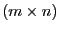 -dimensionale Matrix ist und
-dimensionale Matrix ist und
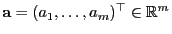 .
.
Theorem 2.3

Für jedes
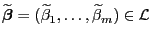
gilt
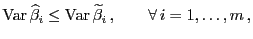 |
(14) |
wobei die Gleichheit in
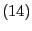
genau dann für jedes
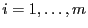
gilt, wenn
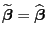
.
- Beweis
-
- Weil vorausgesetzt wird, dass der lineare Schätzer
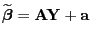 erwartungstreu für
erwartungstreu für
 ist, gilt
für jedes
ist, gilt
für jedes
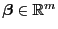 , wobei sich die letzte Gleichheit aus
, wobei sich die letzte Gleichheit aus
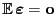 ergibt.
ergibt.
- Hieraus folgt, dass
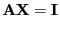 und und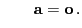 |
(15) |
- Somit gilt
d.h., jeder lineare erwartungstreue Schätzer
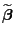 für
für
 hat die Form
hat die Form
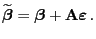 |
(16) |
- Für die Kovarianzmatrix
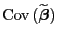 des
Zufallsvektors
des
Zufallsvektors
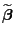 gilt also
d.h.
gilt also
d.h.
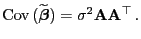 |
(17) |
- Außerdem ergibt sich aus (17) ergibt sich mit
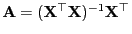 ,
dass die Kovarianzmatrix
,
dass die Kovarianzmatrix
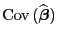 des KQ-Schätzers
des KQ-Schätzers
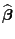 gegeben ist durch
gegeben ist durch
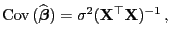 |
(18) |
denn es gilt
- Um die Gültigkeit von (14) zu beweisen, ist somit
zu zeigen, dass
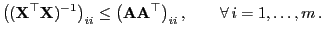 |
(19) |
- Mit
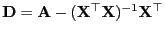 gilt
gilt
denn wegen (15) gilt
wobei 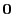 die Nullmatrix bezeichnet.
die Nullmatrix bezeichnet.
- Weil mit
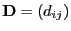 die Ungleichung
die Ungleichung
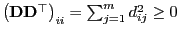 gilt, ergibt sich hieraus die Gültigkeit von (19).
gilt, ergibt sich hieraus die Gültigkeit von (19).
- Außerdem wird klar, dass die Gleichheit in (19) für
jedes
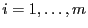 genau dann gilt, wenn
genau dann gilt, wenn
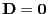 , d.h.
, d.h.
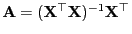 .
.

- Beachte
-
Theorem 2.4
Sei
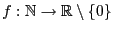
eine Funktion mit
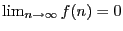
, so dass der Grenzwert
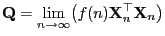 |
(20) |
existiert und die
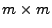
Matrix
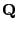
invertierbar ist.
Dann ist
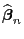
ein schwach konsistenter Schätzer
für

.
- Beweis
-
- Weil
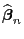 erwartungstreu ist (vgl.
Theorem 2.2), gilt für jedes
erwartungstreu ist (vgl.
Theorem 2.2), gilt für jedes 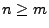
wobei sich die letzte Abschätzung aus der
Tschebyschev-Ungleichung ergibt (vgl. Theorem WR-4.18).
- Es genügt somit zu zeigen, dass
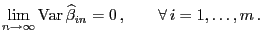 |
(21) |
- Die Matrix
 ist wohldefiniert, weil vorausgesetzt
wird, dass die (Grenz-) Matrix
ist wohldefiniert, weil vorausgesetzt
wird, dass die (Grenz-) Matrix
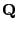 invertierbar ist. Außerdem
ergibt sich aus (20), dass
invertierbar ist. Außerdem
ergibt sich aus (20), dass
- Aus der in (18) hergeleiteten Formel für die
Kovarianzmatrix des Zufallsvektors
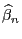 ergibt sich
nun, dass
ergibt sich
nun, dass
- Hieraus ergibt sich insbesondere die Gültigkeit von
(21).





Nächste Seite: Erwartungstreue Schätzung der Varianz
Aufwärts: Methode der kleinsten Quadrate
Vorherige Seite: Normalengleichung
Inhalt
Hendrik Schmidt
2006-02-27
![]() vollen (Spalten-) Rang hat
und leiten drei verschiedene Güteeigenschaften des in
(10) gegebenen KQ-Schätzers
vollen (Spalten-) Rang hat
und leiten drei verschiedene Güteeigenschaften des in
(10) gegebenen KQ-Schätzers
![]() her.
her.
![]() besitzt außerdem die
folgende Eigenschaft der Varianzminimalität. Dabei bezeichne
besitzt außerdem die
folgende Eigenschaft der Varianzminimalität. Dabei bezeichne
![]() die Familie aller erwartungstreuen linearen Schätzer
die Familie aller erwartungstreuen linearen Schätzer
![]() für
für
![]() , wobei
, wobei
![]() eine
eine
![]() -dimensionale Matrix ist und
-dimensionale Matrix ist und
![]() .
.