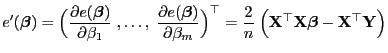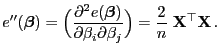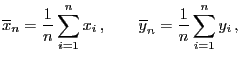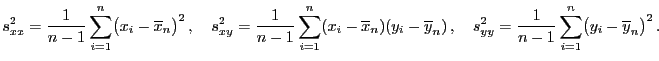Nächste Seite: Güteeigenschaften des KQ-Schätzers
Aufwärts: Methode der kleinsten Quadrate
Vorherige Seite: Methode der kleinsten Quadrate
Inhalt
Normalengleichung
Man kann leicht zeigen, dass die in (8)
betrachtete Funktion
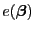 ein eindeutig bestimmtes
Minimum hat, wenn die Designmatrix
ein eindeutig bestimmtes
Minimum hat, wenn die Designmatrix
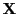 vollen (Spalten-)
Rang hat, d.h., wenn
vollen (Spalten-)
Rang hat, d.h., wenn
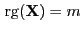 gilt.
gilt.
Theorem 2.1

Sei
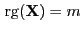
.
- Der mittlere quadratische Fehler
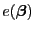 in
in
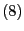 ist genau dann minimal, wenn
ist genau dann minimal, wenn
 Lösung der folgenden Normalengleichung ist:
Lösung der folgenden Normalengleichung ist:
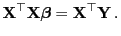 |
(9) |
- Dabei hat
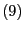 die eindeutig bestimmte Lösung
die eindeutig bestimmte Lösung
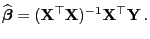 |
(10) |
- Beweis
-
- Beachte
 Der Schätzer
Der Schätzer
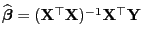 für
für
 ist eine Lineartransformation der Zufallsstichprobe
ist eine Lineartransformation der Zufallsstichprobe
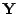 , d.h.,
, d.h.,
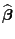 ist ein linearer Schätzer.
ist ein linearer Schätzer.
- Beispiele
 (einfaches und multiples lineares Regressionsmodell)
(einfaches und multiples lineares Regressionsmodell)




Nächste Seite: Güteeigenschaften des KQ-Schätzers
Aufwärts: Methode der kleinsten Quadrate
Vorherige Seite: Methode der kleinsten Quadrate
Inhalt
Hendrik Schmidt
2006-02-27
![]() ein eindeutig bestimmtes
Minimum hat, wenn die Designmatrix
ein eindeutig bestimmtes
Minimum hat, wenn die Designmatrix
![]() vollen (Spalten-)
Rang hat, d.h., wenn
vollen (Spalten-)
Rang hat, d.h., wenn
![]() gilt.
gilt.