



Nächste Seite: Methode der kleinsten Quadrate
Aufwärts: skript
Vorherige Seite: Verteilungs- und Unabhängigkeitseigenschaften linearer
Inhalt
Lineare Modelle; Designmatrix mit vollem Rang
Zur Erinnerung (vgl. Kapitel 5 der Vorlesung ,,Statistik
I''):
- Bei der einfachen
linearen Regression wird von zwei Datensätzen
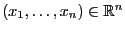 und
und
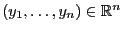 ausgegangen, die stochastisch modelliert werden sollen.
ausgegangen, die stochastisch modelliert werden sollen.
- Dabei fassen wir die Vektoren
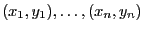 als
Realisierungen von
als
Realisierungen von  Zufallsvektoren
Zufallsvektoren
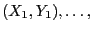
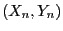 auf, die typischerweise nicht identisch verteilt
sind.
auf, die typischerweise nicht identisch verteilt
sind.
- Wir deuten die Zufallsvariablen
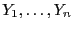 als Zielvariablen und nehmen an, dass sie auf die folgende Weise von
den Ausgangsvariablen
als Zielvariablen und nehmen an, dass sie auf die folgende Weise von
den Ausgangsvariablen
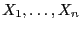 abhängen:
abhängen:
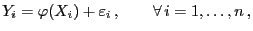 |
(1) |
wobei
-
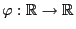 eine beliebige (Borel-messbare) Funktion, die
so genannte Regressionsfunktion ist und
eine beliebige (Borel-messbare) Funktion, die
so genannte Regressionsfunktion ist und
-
 Zufallsvariablen, so genannte
Störgrößen sind, durch die beispielsweise zufällige
Messfehler modelliert werden können.
Zufallsvariablen, so genannte
Störgrößen sind, durch die beispielsweise zufällige
Messfehler modelliert werden können.
- Ein wichtiger Spezialfall liegt vor, wenn die Regressionsfunktion
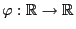 eine lineare Funktion ist, die so genannte
Regressionsgerade, d.h., wenn es reelle Zahlen
eine lineare Funktion ist, die so genannte
Regressionsgerade, d.h., wenn es reelle Zahlen
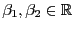 gibt mit
gibt mit
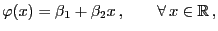 |
(2) |
wobei 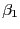 die Regressionskonstante und
die Regressionskonstante und 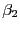 der
Regressionskoeffizient genannt wird.
der
Regressionskoeffizient genannt wird.
- Die Größen
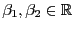 sind unbekannte
Modellparameter, die aus den beobachteten Daten
sind unbekannte
Modellparameter, die aus den beobachteten Daten
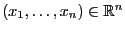 und
und
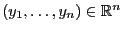 geschätzt werden sollen.
geschätzt werden sollen.
Wir betrachten nun die folgende multivariate
Verallgemeinerung des einfachen linearen Regressionsmodells, wobei
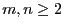 beliebige natürliche Zahlen seien, so dass
beliebige natürliche Zahlen seien, so dass 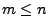 .
.
- Wir nehmen an, dass die Zielvariablen
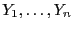 von vektoriellen
von vektoriellen 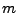 -dimensionalen Ausgangsvariablen
-dimensionalen Ausgangsvariablen
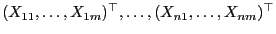 abhängen, d.h., es gelte
abhängen, d.h., es gelte
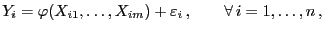 |
(3) |
wobei
- Dabei betrachten wir hier nur den Fall, dass die Ausgangsvariablen
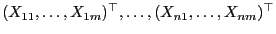 deterministisch sind, d.h., es gelte
für gewisse Vektoren
deterministisch sind, d.h., es gelte
für gewisse Vektoren
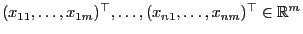 .
.
- Beachte
-
- In Matrixschreibweise lässt sich dann das in (3)
und (4) gegebene Modell wie folgt formulieren:
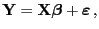 |
(6) |
wobei
 |
(7) |
- Dabei wird
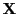 die Designmatrix des Regressionsmodells
genannt.
die Designmatrix des Regressionsmodells
genannt.
Unterabschnitte




Nächste Seite: Methode der kleinsten Quadrate
Aufwärts: skript
Vorherige Seite: Verteilungs- und Unabhängigkeitseigenschaften linearer
Inhalt
Hendrik Schmidt
2006-02-27
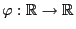 eine beliebige (Borel-messbare) Funktion, die
so genannte Regressionsfunktion ist und
eine beliebige (Borel-messbare) Funktion, die
so genannte Regressionsfunktion ist und
 Zufallsvariablen, so genannte
Störgrößen sind, durch die beispielsweise zufällige
Messfehler modelliert werden können.
Zufallsvariablen, so genannte
Störgrößen sind, durch die beispielsweise zufällige
Messfehler modelliert werden können.
![]() beliebige natürliche Zahlen seien, so dass
beliebige natürliche Zahlen seien, so dass ![]() .
.