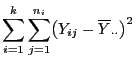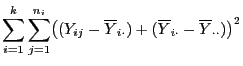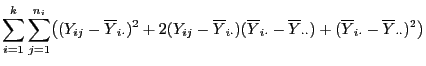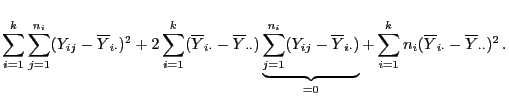Nächste Seite: Reparametrisierung der Erwartungswerte
Aufwärts: Varianzanalyse als lineares Modell
Vorherige Seite: Varianzanalyse als lineares Modell
Inhalt
Einfaktorielle Varianzanalyse; ANOVA-Nullhypothese
- Beachte
-
- Die Nummern
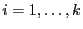 der Klassen
der Klassen
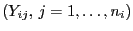 werden als Stufen eines Einflussfaktors
gedeutet.
werden als Stufen eines Einflussfaktors
gedeutet.
- Die oben gemachten Modellannahmen bedeuten insbesondere, dass die
beobachteten Werte
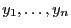 der Zielvariablen
der Zielvariablen
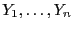 wie folgt tabellarisch strukturiert werden
können:
wie folgt tabellarisch strukturiert werden
können:
Wir zeigen, dass die klassische ANOVA-Nullhypothese
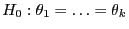 mit Hilfe von so genannten
Kontrasten ausgedrückt werden kann.
mit Hilfe von so genannten
Kontrasten ausgedrückt werden kann.
Lemma 3.1

Seien
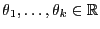
beliebige relle Zahlen. Für
die Gültigkeit von
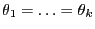
ist dann notwendig
und hinreichend, dass
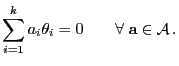 |
(6) |
- Beweis
-
- Beachte
-
Durch die folgende Quadratsummenzerlegung ergibt sich eine
anschauliche Deutung von Zähler und Nenner der in
(8) betrachteten Testgröße
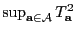 , vgl. auch
Theorem 2.9.
, vgl. auch
Theorem 2.9.
- Beweis
 Durch Ausmultiplizieren der linken Seite von (9)
ergibt sich, dass
Durch Ausmultiplizieren der linken Seite von (9)
ergibt sich, dass

- Beachte
-
- Die Doppelsumme auf der linken Seite von (9) kann
als eine Maßzahl für die (Gesamt-) Variabilität der
Stichprobenvariablen
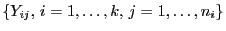 aufgefasst werden.
aufgefasst werden.
- Die erste Summe auf der rechten Seite von (9) ist
eine Maßzahl für die Variabilität zwischen den Stufen des
Einflussfaktors, während die Doppelsumme auf der rechten Seite von
(9) eine Maßzahl für die Variabilität innerhalb der Stufen des Einflussfaktors ist.
- Wegen der in (7) gegebenen Definition von
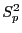 ist die in (8) betrachtete Testgröße also
proportional zu dem Quotienten, der aus der Variabilität zwischen
den Stufen des Einflussfaktors und der Variabilität innerhalb der
Stufen gebildet wird.
ist die in (8) betrachtete Testgröße also
proportional zu dem Quotienten, der aus der Variabilität zwischen
den Stufen des Einflussfaktors und der Variabilität innerhalb der
Stufen gebildet wird.
- Die ANOVA-Nullhypothese
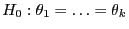 wird somit
abgelehnt, wenn die Variabilität zwischen den Stufen signifikant
größer als die Variabilität innerhalb der Stufen des
Einflussfaktors ist.
wird somit
abgelehnt, wenn die Variabilität zwischen den Stufen signifikant
größer als die Variabilität innerhalb der Stufen des
Einflussfaktors ist.




Nächste Seite: Reparametrisierung der Erwartungswerte
Aufwärts: Varianzanalyse als lineares Modell
Vorherige Seite: Varianzanalyse als lineares Modell
Inhalt
Hendrik Schmidt
2006-02-27
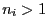 für jedes
für jedes
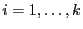 und
und
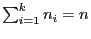
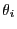 haben
mögen.
haben
mögen.
![]() mit Hilfe von so genannten
Kontrasten ausgedrückt werden kann.
mit Hilfe von so genannten
Kontrasten ausgedrückt werden kann.
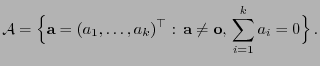
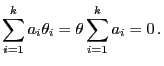
![]() , vgl. auch
Theorem 2.9.
, vgl. auch
Theorem 2.9.