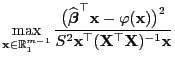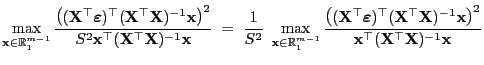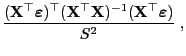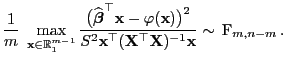Nächste Seite: Beliebige Designmatrix; verallgemeinerte Inverse
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Konfidenzbereiche; Prognose von Zielvariablen
Inhalt
Konfidenzband
In diesem Abschnitt nehmen wir an, dass die Designmatrix
 die Form
die Form
 |
(63) |
hat, d.h., wir betrachten das (multiple) lineare
Regressionsmodell.
- In der Definitionsgleichung (4) für die
Regressionsfunktion
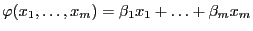 setzen wir nun
setzen wir nun 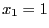 und bestimmen ein Konfidenzband für die Regressionshyperebene
und bestimmen ein Konfidenzband für die Regressionshyperebene
- Dabei ist eine Zahl
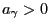 gesucht, so dass mit der
vorgegebenen (Überdeckungs-) Wahrscheinlichkeit
gesucht, so dass mit der
vorgegebenen (Überdeckungs-) Wahrscheinlichkeit
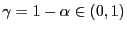
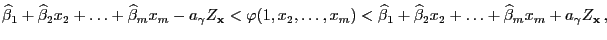 |
(64) |
gleichzeitig für jedes
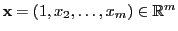 gilt,
wobei
gilt,
wobei
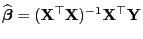
und
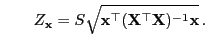
Bei der Lösung dieser Fragestellung ist das folgende Hilfsergebnis
nützlich.
Lemma 2.4

Mit Wahrscheinlichkeit
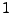
gilt
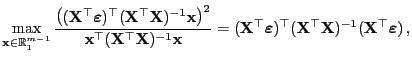 |
(65) |
wobei
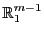
die Menge aller derjenigen Vektoren
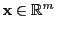
mit
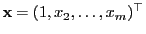
bezeichnet.
- Beweis
-
Aus dem folgenden Resultat, das eine vektorielle Verallgemeinerung
von Theorem I-5.9 ist, ergibt sich das gesuchte Konfidenzband.
- Beweis
-
- Für jedes
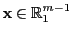 gilt
gilt
und somit
wobei sich die letzte Gleichheit aus Lemma 2.4
ergibt.
- Es gilt also
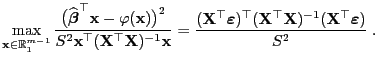 |
(69) |
- Weil
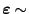 N
N
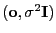 und weil
ergibt sich aus Theorem 1.10, dass
und weil
ergibt sich aus Theorem 1.10, dass
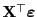 und
und
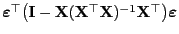 unabhängig sind.
unabhängig sind.
- Aus der bereits im Beweis von Theorem 2.7
hergeleiteten Darstellungsformel
ergibt sich somit, dass auch die Zufallsvariablen
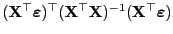 und
und 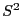 unabhängig sind.
unabhängig sind.
- In Theorem 2.7 hatten wir gezeigt, dass
- Außerdem ergibt sich aus Theorem 1.9, dass
weil die
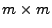 (Kovarianz-) Matrix
(Kovarianz-) Matrix
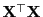 des
normalverteilten Zufallsvektors
des
normalverteilten Zufallsvektors
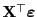 vollen Rang hat
und weil die Matrix
vollen Rang hat
und weil die Matrix
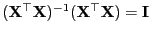 idempotent ist.
idempotent ist.
- Wegen (69) haben wir also insgesamt gezeigt, dass
- Für den in (64) bzw. (68)
betrachteten Schwellenwert ergibt sich deshalb
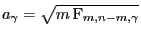 .
.





Nächste Seite: Beliebige Designmatrix; verallgemeinerte Inverse
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Konfidenzbereiche; Prognose von Zielvariablen
Inhalt
Hendrik Schmidt
2006-02-27
![]() die Form
die Form