



Nächste Seite: Beispiele
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Tests linearer Hypothesen
Inhalt
Konfidenzbereiche
- Bei der Konstruktion von Konfidenzbereichen gehen wir ähnlich wie
in Abschnitt 2.2.4 vor, wo der Fall betrachtet wurde,
dass die Designmatrix
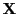 vollen Rang
vollen Rang
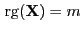 hat.
Dabei nehmen wir jetzt allerdings so wie in
Abschnitt 3.3.2 an, dass
hat.
Dabei nehmen wir jetzt allerdings so wie in
Abschnitt 3.3.2 an, dass
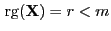 .
.
- Sei
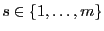 , und
, und
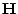 sei eine
sei eine 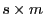 Matrix
mit vollem Rang
Matrix
mit vollem Rang
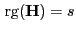 , deren Eintragungen bekannt seien,
wobei
, deren Eintragungen bekannt seien,
wobei
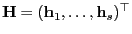 .
.
- Dann ergibt sich unmittelbar aus Theorem 3.15 der
folgende Konfidenzbereich für den Vektor
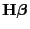 zum Niveau
zum Niveau
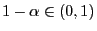 .
.
Theorem 3.17

Sämtliche Komponenten
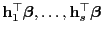
des Vektors
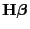
seien schätzbare Funktionen von

. Dann
ist der (zufällige) Ellipsoid
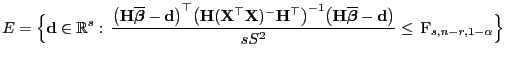 |
(77) |
ein Konfidenzbereich für
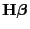
zum Niveau
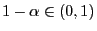
, wobei
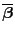
und
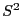
die in
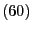
bzw.
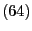
gegebenen
Schätzer für

bzw.
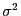
sind.
Aus Theorem 3.17 ergibt sich insbesondere das
folgende Resultat.
Korollar 3.1

Für jedes
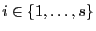
ist durch
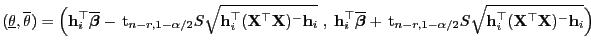 |
(78) |
ein Konfidenzintervall
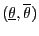
für
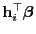
zum Niveau
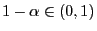
gegeben.
- Beispiel
-
- Wir betrachten das folgende lineare Modell, vgl. N. Ravishanker
und D.K. Dey (2002) A First Course in Linear Model Theory,
Chapman & Hall/CRC, S. 235:
wobei
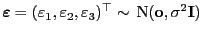 .
.
- Mit Hilfe von Korollar 3.1 soll ein
Konfidenzintervall für
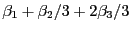 zum Niveau
zum Niveau
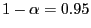 bestimmt werden.
bestimmt werden.
- Weil
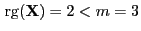 , muss zunächst geprüft werden, ob
, muss zunächst geprüft werden, ob
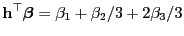 |
(79) |
mit
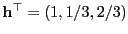 eine erwartungstreu schätzbare
Funktion von
eine erwartungstreu schätzbare
Funktion von
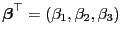 ist.
ist.
- Außerdem gilt
und eine verallgemeinerte Inverse von
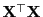 ist
gegeben durch:
ist
gegeben durch:
- Hieraus folgt, dass
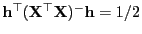 und
und
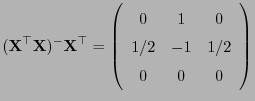
bzw.
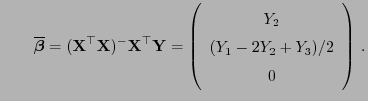
- Somit ergibt sich, dass
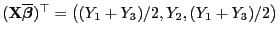 bzw.
bzw.
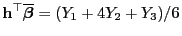
und
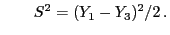
- Das gesuchte Konfidenzintervall
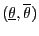 für
für
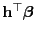 zum
Niveau
zum
Niveau
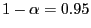 hat also die Form
wobei
hat also die Form
wobei
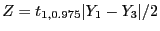 .
.
In Verallgemeinerung von Theorem 2.12 leiten wir nun
ein so genanntes Scheffé-Konfidenzband her, d.h. simultane
Konfidenzintervalle für eine ganze Klasse von schätzbaren
Funktionen des Parametervektors
 .
.
- Beweis
-
- Ähnlich wie im Beweis von Theorem 2.12 ergibt sich
aus der Ungleichung von Cauchy-Schwarz für Skalarprodukte, vgl.
(66), dass
wobei sich das Maximum über sämtliche Vektoren
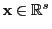 mit
mit
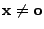 erstreckt.
erstreckt.
- Hieraus und aus Theorem 3.15 ergibt sich nun, dass





Nächste Seite: Beispiele
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Tests linearer Hypothesen
Inhalt
Hendrik Schmidt
2006-02-27
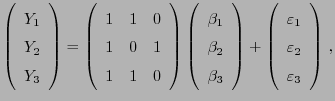
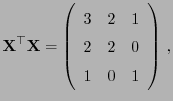
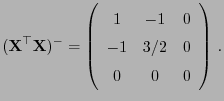
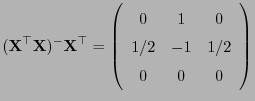 bzw.
bzw.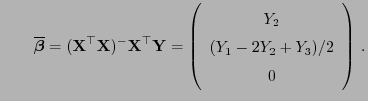
![]() .
.