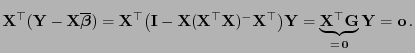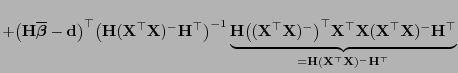Nächste Seite: Konfidenzbereiche
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Tests linearer Hypothesen
In diesem Abschnitt diskutieren wir eine verallgemeinerte Version
des Tests für Linearformen von
 , den wir in
Abschnitt 2.2.3 für den Fall von Designmatrizen
, den wir in
Abschnitt 2.2.3 für den Fall von Designmatrizen
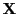 mit vollem Spaltenrang betrachtet hatten, vgl.
Theorem 2.11. Jetzt nehmen wir dagegen an, dass
mit vollem Spaltenrang betrachtet hatten, vgl.
Theorem 2.11. Jetzt nehmen wir dagegen an, dass
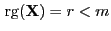 .
.
- Definition
 Die Hypothese
Die Hypothese
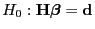 heißt testbar, wenn
sämtliche Komponenten
heißt testbar, wenn
sämtliche Komponenten
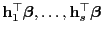 des Vektors
des Vektors
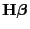 schätzbare Funktionen des Parametervektors
schätzbare Funktionen des Parametervektors
 sind.
sind.
- Beachte
 Aus Theorem 3.9 folgt, dass die Hypothese
Aus Theorem 3.9 folgt, dass die Hypothese
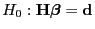 genau dann testbar ist, wenn
genau dann testbar ist, wenn
- es eine
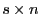 Matrix
Matrix
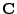 gibt, so dass
gibt, so dass
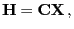 |
(69) |
bzw.
- die Matrix
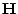 der folgenden Gleichung genügt:
der folgenden Gleichung genügt:
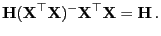 |
(70) |
Bei der Konstruktion einer Testgröße zur Verifizierung der in
(68) betrachteten Nullhypothese
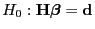 ist der folgende Hilfssatz nützlich.
ist der folgende Hilfssatz nützlich.
Lemma 3.9
- Sei
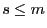 , sei
, sei
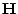 eine
eine 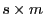 Matrix mit vollem Rang
Matrix mit vollem Rang
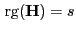 , die der Gleichung
, die der Gleichung
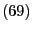 bzw.
bzw.
 genügt, und sei
genügt, und sei
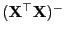 eine
beliebige verallgemeinerte Inverse von
eine
beliebige verallgemeinerte Inverse von
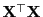 .
.
- Dann ist die
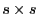 Matrix
Matrix
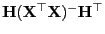 positiv definit (und damit
invertierbar).
positiv definit (und damit
invertierbar).
- Beweis
-
- Beachte
-
Theorem 3.15

Die Hypothese
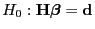
sei testbar. Unter
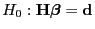
gilt dann
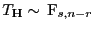
,
d.h., die in
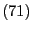
gegebene Testgröße
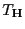
ist F-verteilt mit
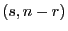
Freiheitsgraden.
- Beweis
-
- Beachte
-
- Die Wahl der Testgröße
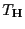 in (71) kann
wie folgt motiviert werden: Ähnlich wie im Beweis von
Theorem 3.15 ergibt sich aus
Theorem 1.9, dass die quadratische Form
in (71) kann
wie folgt motiviert werden: Ähnlich wie im Beweis von
Theorem 3.15 ergibt sich aus
Theorem 1.9, dass die quadratische Form
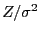 mit
im allgemeinen (d.h., ohne die Gültigkeit von
mit
im allgemeinen (d.h., ohne die Gültigkeit von
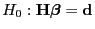 vorauszusetzen) eine nichtzentrale
vorauszusetzen) eine nichtzentrale
 -Verteilung
-Verteilung
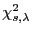 hat mit
hat mit
- Hieraus folgt, dass
wobei sich die letzte Gleichheit aus der Formel für die
momenterzeugende Funktion der
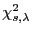 -Verteilung
ergibt, die im Beweis von Theorem 1.8 hergeleitet
wurde.
-Verteilung
ergibt, die im Beweis von Theorem 1.8 hergeleitet
wurde.
- Andererseits ergibt sich aus Lemma 1.8 und
Lemma 3.9, dass die inverse Matrix
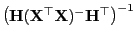 positiv
definit ist und dass somit
wenn die Hypothese
positiv
definit ist und dass somit
wenn die Hypothese
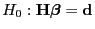 falsch ist. Aus
(72) folgt dann in diesem Fall, dass
falsch ist. Aus
(72) folgt dann in diesem Fall, dass
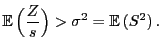 |
(73) |
- Allgemein gilt (wegen der Unabhängigkeit von
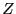 und
und 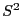 ), dass
), dass
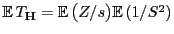 ,
und aus der Jensen-Ungleichung folgt, dass
,
und aus der Jensen-Ungleichung folgt, dass
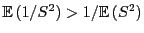 .
.
- Aus (73) ergibt sich somit, dass
wenn
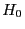 falsch ist.
falsch ist.
- Es liegt deshalb nahe, die Nullhypothese
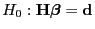 abzulehnen, wenn die Testgröße
abzulehnen, wenn die Testgröße
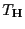 Werte annimmt, die signifikant größer als
Werte annimmt, die signifikant größer als 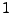 sind.
sind.
- Wegen der in Theorem 3.15 hergeleiteten
Verteilungseigenschaft der Testgröße
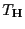 wird somit
wird somit 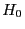 abgelehnt, wenn
abgelehnt, wenn
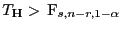 .
.
In manchen Fällen ist es zweckmäßiger, eine alternative
Darstellung der in (71) gegebenen Testgröße
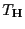 zu betrachten. Hierfür definieren wir die folgenden
beiden Summen von quadratischen Abweichungen
zu betrachten. Hierfür definieren wir die folgenden
beiden Summen von quadratischen Abweichungen 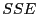 bzw.
bzw.
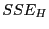 (Sums of Squared Errors) mit
(Sums of Squared Errors) mit
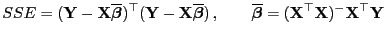 |
(74) |
und
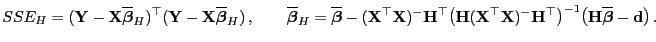 |
(75) |
- Beweis
-
- Es gilt
weil sich aus den Teilaussagen 1 und 2 von Lemma 3.8
ergibt, dass
- Aus (69), d.h.
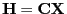 , und aus
Lemma 3.7 ergibt sich somit, dass
, und aus
Lemma 3.7 ergibt sich somit, dass

- Beachte
-
- Aus der Definitionsgleichung (75) von
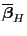 ergibt sich, dass
d.h., der in (75) gegebene Zufallsvektor
ergibt sich, dass
d.h., der in (75) gegebene Zufallsvektor
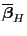 nimmt nur Werte in dem eingeschränkten
Parameterraum
nimmt nur Werte in dem eingeschränkten
Parameterraum
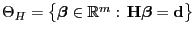 an.
an.
- Außerdem kann man leicht zeigen, dass
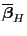 den
mittleren quadratischen Fehler
den
mittleren quadratischen Fehler
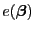 für alle
für alle
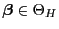 minimiert, wobei
minimiert, wobei




Nächste Seite: Konfidenzbereiche
Aufwärts: Normalverteilte Störgrößen
Vorherige Seite: Maximum-Likelihood-Schätzer
Inhalt
Hendrik Schmidt
2006-02-27
![]() , den wir in
Abschnitt 2.2.3 für den Fall von Designmatrizen
, den wir in
Abschnitt 2.2.3 für den Fall von Designmatrizen
![]() mit vollem Spaltenrang betrachtet hatten, vgl.
Theorem 2.11. Jetzt nehmen wir dagegen an, dass
mit vollem Spaltenrang betrachtet hatten, vgl.
Theorem 2.11. Jetzt nehmen wir dagegen an, dass
![]() .
.
![]() ist der folgende Hilfssatz nützlich.
ist der folgende Hilfssatz nützlich.
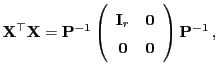
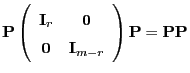
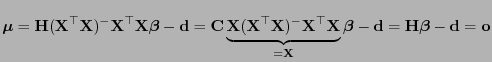
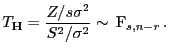
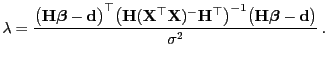
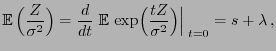
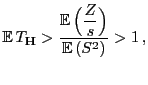
![]() zu betrachten. Hierfür definieren wir die folgenden
beiden Summen von quadratischen Abweichungen
zu betrachten. Hierfür definieren wir die folgenden
beiden Summen von quadratischen Abweichungen ![]() bzw.
bzw.
![]() (Sums of Squared Errors) mit
(Sums of Squared Errors) mit