



Nächste Seite: Fisher-Informationsmatrix und zentraler Grenzwertsatz
Aufwärts: -Anpassungstest von Pearson-Fisher
Vorherige Seite: Pearson-Fisher-Teststatistik
Inhalt
Multivariater zentraler Grenzwertsatz für
ML-Schätzer
Ähnlich wie in Abschnitt I-2.4.2, wo der Fall 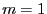 betrachtet
wurde, lässt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
betrachtet
wurde, lässt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
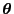 herleiten.
herleiten.
Dabei werden die folgenden Regularitätsbedingungen benötigt.
- Beachte
-
- Zur Erinnerung :
- Im Allgemeinen wird der Maximum-Likelihood-Schätzer
 für
für
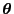 als Lösung des folgenden Optimierungsproblems
definiert (vgl. Abschnitt I-2.2.2).
als Lösung des folgenden Optimierungsproblems
definiert (vgl. Abschnitt I-2.2.2).
- Dabei ist
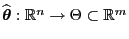 eine
Stichprobenfunktion mit
eine
Stichprobenfunktion mit
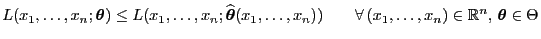 |
(57) |
und
- Unter den obengenannten Regularitätsbedingungen kann man zeigen,
dass
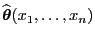 für beliebige
für beliebige
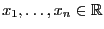 dem folgenden Gleichungssystem genügt:
dem folgenden Gleichungssystem genügt:
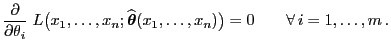 |
(58) |
- Um den multivariaten zentralen Grenzwertsatz formulieren zu
können, benötigen wir den Begriff der Fischer-Informationsmatrix, der bereits in
Abschnitt 4.3.1 eingeführt wurde.
In Verallgemeinerung von Theorem I-2.11, wo der 1-dimensionale
Fall betrachtet wurde, lässt sich für schwach konsistente Folgen
von Maximum-Likelihood-Schätzern
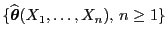 des
Parametervektors
des
Parametervektors
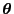 , die dem Gleichungssystem
(58) genügen, der folgende multivariate zentrale
Grenzwertsatz herleiten.
, die dem Gleichungssystem
(58) genügen, der folgende multivariate zentrale
Grenzwertsatz herleiten.
Der Beweis von
Theorem 5.8 verläuft ähnlich wie der Beweis von
Theorem I-2.11. Er wird deshalb hier weggelassen, vgl.
beispielsweise E.L. Lehmann und G. Casella (1998) The Theory
of Point Estimation, Springer-Verlag, New York.




Nächste Seite: Fisher-Informationsmatrix und zentraler Grenzwertsatz
Aufwärts: -Anpassungstest von Pearson-Fisher
Vorherige Seite: Pearson-Fisher-Teststatistik
Inhalt
Hendrik Schmidt
2006-02-27
![]() betrachtet
wurde, lässt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
betrachtet
wurde, lässt sich ein multivariater zentraler Grenzwertsatz
für konsistente Folgen von Maximum-Likelihood-Schätzern des
Parametervektors
![]() herleiten.
herleiten.
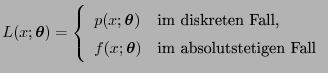
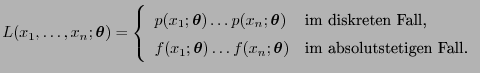
![]() des
Parametervektors
des
Parametervektors
![]() , die dem Gleichungssystem
(58) genügen, der folgende multivariate zentrale
Grenzwertsatz herleiten.
, die dem Gleichungssystem
(58) genügen, der folgende multivariate zentrale
Grenzwertsatz herleiten.