Suffizienz und monotoner Likelihood-Quotient

• Die Familie $\{P_\theta,\theta\in\Theta\}$ bestehe (so wie bisher stets angenommen) entweder nur aus diskreten Verteilungen oder nur aus absolutstetigen Verteilungen, wobei $P_\theta\not=P_{\theta^\prime}$ genau dann, wenn $\theta\not=\theta^\prime$.
• Die Menge $B=\{x\in\mathbb{R}:\, L(x;\theta)>0\}$ hänge nicht von $\theta\in\Theta$ ab, wobei die Likelihood-Funktion $L(x;\theta)$ gegeben ist durch
  $$L(x;\theta)=\left\{\begin{array}{ll} p(x;\theta) & \mbox{im diskr... ... Fall,}\\ f(x;\theta) & \mbox{im absolutstetigen Fall} \end{array}\right.$$
  und $p(x;\theta)$ bzw. $f(x;\theta)$ die Wahrscheinlichkeitsfunktion bzw. Dichte von $P_\theta$ ist.

Beachte

 

• Der in Abschnitt 2.3.3 eingeführte Begriff der Suffizienz von Schätzern ermöglicht es, noch eine weitere (äquivalente) Darstellungsform von NP-Tests zum Prüfen der Hypothesen
  $$H_0:\theta=\theta_0$$   versus$$\qquad H_1:\theta=\theta_1$$
  für zwei vorgegebene Parameterwerte $\theta_0,\theta_1\in\Theta$ mit $\theta_0\not=\theta_1$ anzugeben.
• Sei $\widehat\theta:\mathbb{R}^n\to\mathbb{R}^m$ ein suffizienter Schätzer für $\theta$.
• Aus dem Faktorisierungssatz von Neyman-Fisher (vgl. die Theoreme 2.3 und 2.4) folgt dann, daß es Borel-meßbare Funktionen $g_0,\,g_1:\mathbb{R}^m\to[0,\infty)$ und $h:\mathbb{R}^n\to[0,\infty)$ gibt, so daß

  $$L_i(x)=g_i(\widehat\theta(x))\, h(x)\,,\qquad\forall\, x\in\mathbb{R}^n,\, i=0,1\,.$$ (54)

  
  

Theorem 4.4    

• Sei $\widehat\theta:\mathbb{R}^n\to\mathbb{R}^m$ ein suffizienter Schätzer für $\theta$, und sei
  $$K=\{t\in\mathbb{R}^m:\, g_1(t)> a g_0(t)\}\,,\qquad R=\{t\in\mathbb{R}^m:\, g_1(t)=a g_0(t)\}\,,$$
  wobei $g_i(t)$ durch die Faktorisierung $(\ref{dar.max.lik})$ der Likelihood-Funktion $L_i(x)$ gegeben ist.
• Für beliebige $a\ge 0$ und $q\in[0,1]$ ist dann der Test $\varphi_a:\mathbb{R}^n\to[0,1]$ mit

  $$\varphi_a(x)=\left\{\begin{array}{ll} 1\,, &\mbox{falls $\wideha... ...s $\widehat\theta(x)\in \mathbb{R}^m\setminus(K\cup R) $,} \end{array}\right.$$ (55)

  
  
  bester Test zum Niveau $\alpha=P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)\in K)+qP_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)\in R)$.

Beweis

 

• Wegen (54) gilt für den in (28) definierten Likelihood-Quotient $T(x)$, daß
  $$T(x)=\left\{\begin{array}{ll}\displaystyle \frac{L_1(x)}{L_0(x)}... ...s $L_0(x)>0$\,,}\\ \infty\,,&\mbox{falls $L_0(x)=0$.} \end{array}\right.$$

• Hieraus ergibt sich für fast jedes $x\in\mathbb{R}^n$, daß $\widehat\theta(x)\in K$ genau dann, wenn $T(x)>a$, und $\widehat\theta(x)\in R$ genau dann, wenn $T(x)=a$.
• Aus Theorem 4.1 folgt nun, daß der in (55) gegebene Test $\varphi_a:\mathbb{R}^n\to[0,\infty)$ bester Test zum Niveau $\alpha=P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)\in K)+qP_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)\in R)$ ist.
  
  $\Box$

Beachte

 

• Die in (39), (40) bzw. (44) betrachteten Beispiele von NP-Tests hängen nicht vom Parameterwert $\lambda_1$ bzw. $\mu_1$ der Alternativhypothese $H_1$ ab.
• Um diese Unabhängigkeitseigenschaft in einer allgemeineren Form formulieren zu können, ist neben der Suffizienz von Schätzern noch die folgende Begriffsbildung nützlich.

Definition

 

• Sei $\Theta\subset\mathbb{R}$. Man sagt, daß $\{P_\theta,\theta\in\Theta\}$ eine parametrische Verteilungsfamilie mit monotonem Likelihood-Quotient in $\widehat\theta$ ist, falls es
  • für jedes $n\in\mathbb{N}$ eine Borel-meßbare Abbildung $\widehat\theta:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\}$ und
  • für beliebige $\theta,\theta^\prime\in\Theta$ eine nichtnegative Funktion $g(t,\theta,\theta^\prime),\, t\in\mathbb{R}\cup\{\infty\}$ gibt, die stetig und streng monoton in $t$ ist (und zwar monoton wachsend, falls $\theta<\theta^\prime$, bzw. monoton fallend, falls $\theta>\theta^\prime$), so daß

    $$\frac{L(x_1;\theta^\prime)\ldots L(x_n;\theta^\prime) }{L(x_1;\t... ...a(x);\theta,\theta^\prime\bigr)\,,\qquad\forall\,x=(x_1,\ldots,x_n)\in B^n \,.$$ (56)

    
    

• Dabei setzen wir für $x=(x_1,\ldots,x_n)\in \mathbb{R}^n\setminus B^n$
  $$\frac{L(x_1;\theta^\prime)\ldots L(x_n;\theta^\prime) }{L(x_1;\theta)\ldots L(x_n;\theta)}=\widehat\theta(x)=\infty\,.$$

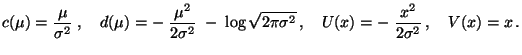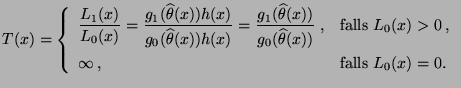
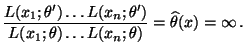
Für parametrische Verteilungsfamilien mit monotonem Likelihood-Quotient ergibt sich das folgende Resultat unmittelbar aus Theorem 4.4.

Korollar 4.1    

• Sei $\Theta\subset\mathbb{R}$, und sei $H_0:\theta=\theta_0$ bzw. $H_1:\theta=\theta_1$ für zwei vorgegebene Parameterwerte $\theta_0,\theta_1\in\Theta$ mit $\theta_0<\theta_1$.
• Außerdem sei $\widehat\theta:\mathbb{R}^n\to\mathbb{R}$ ein suffizienter Schätzer für $\theta$, und sei $\{P_\theta,\theta\in\Theta\}$ eine parametrische Verteilungsfamilie mit monotonem Likelihood-Quotient in $\widehat\theta$.
• Für beliebige $a^*\in\mathbb{R}$ und $q^*\in[0,1]$ ist dann der Test $\varphi^*:\mathbb{R}^n\to[0,1]$ mit

  $$\varphi^*(x)=\left\{\begin{array}{ll} 1\,, &\mbox{falls $\wideha... ...x)=a^*$,}\\ 0\,, &\mbox{falls $\widehat\theta(x)<a^* $,} \end{array}\right.$$ (57)

  
  
  bester Test zum Niveau $\alpha=P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)>a^*) +q^* P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)=a^*)$.

Beweis

 

• Für $a\ge 0$ seien $K=\{t\in\mathbb{R}:\, g_1(t)> a g_0(t)\}$ und $R=\{t\in\mathbb{R}:\, g_1(t)=a g_0(t)\}$ die in Theorem 4.4 betrachteten Mengen.
• Wegen der in (56) vorausgesetzten Stetigkeits- und Monotonieeigenschaft gilt $\widehat\theta(x)\in K$ genau dann, wenn $\widehat\theta(x)>a^*$, und $\widehat\theta(x)\in R$ genau dann, wenn $\widehat\theta(x)=a^*$, wobei $a\ge 0$ so gewählt ist, daß
  $$a^*=\inf\bigl\{t\in\mathbb{R}:\,g_1(t)> a g_0(t)\bigr\}\,.$$

• Aus Theorem 4.4 folgt somit die Behauptung.
  
  $\Box$

Beachte

 

• Der Test $\varphi^*$ in (57) hängt nicht vom Parameterwert $\theta_1$ der Alternativhypothese $H_1$ ab.
• Falls $\theta_0>\theta_1$, dann läßt sich auf die gleiche Weise wie in Korollar 4.1 zeigen, daß durch

  $$\varphi^*(x)=\left\{\begin{array}{ll} 1\,, &\mbox{falls $\wideha... ...x)=a^*$,}\\ 0\,, &\mbox{falls $\widehat\theta(x)>a^* $,} \end{array}\right.$$ (58)

  
  
  ein bester Test zum Niveau $\alpha=P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)<a^*) +q^* P_{\theta_0}\bigl(\widehat\theta(X_1,\ldots,X_n)=a^*)$ gegeben ist, um die Hypothesen $H_0:\theta=\theta_0$ bzw. $H_1:\theta=\theta_1$ zu prüfen.

Wir zeigen nun, daß Exponentialfamilien unter bestimmten Bedingungen einen monotonen Likelihood-Quotient besitzen.

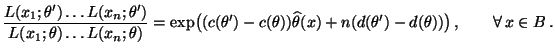
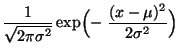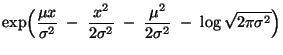Theorem 4.5   Falls $\{P_\theta,\theta\in\Theta\}$ einer einparametrischen Exponentialfamilie angehört, d.h., es gibt Borel-meßbare Funktionen $d,c:\Theta\to\mathbb{R}$ und $U,V:\mathbb{R}\to\mathbb{R}$, so daß

$$L(x;\theta)=\exp\bigl(c(\theta)V(x)+d(\theta)+ U(x)\bigr){1\hspace{-1mm}{\rm I}}_B(x)\,,\qquad\forall\, x\in \mathbb{R}\,,$$ (59)

und falls $c:\Theta\to\mathbb{R}$ streng monoton wachsend ist, dann ist $\{P_\theta,\theta\in\Theta\}$ eine parametrische Verteilungsfamilie mit monotonem Likelihood-Quotient in $\widehat\theta$, wobei $\widehat\theta(x_1,\ldots,x_n)=V(x_1)+\ldots+V(x_n)$.

Beweis

 

• Für $\theta,\theta^\prime\in\Theta$ mit $\theta<\theta^\prime$ ergibt sich aus (59), daß
  $$\frac{L(x_1;\theta^\prime)\ldots L(x_n;\theta^\prime) }{L(x_1;\t... ...at\theta(x) +n(d(\theta^\prime)-d(\theta))\bigr)\,,\qquad\forall\, x\in B\,.$$

• Wegen $c(\theta^\prime)-c(\theta)>0$ ist die Funktion
  $$g(t;\theta,\theta^\prime)=\exp\bigl((c(\theta^\prime)-c(\theta))t +n(d(\theta^\prime)-d(\theta))\bigr)$$
  stetig und streng monoton wachsend in $t$.
• Hieraus folgt, daß der Quotient $\bigl(L(x_1;\theta^\prime)\ldots L(x_n;\theta^\prime)\bigr)\big/\bigl(L(x_1;\theta)\ldots L(x_n;\theta)\bigr)$ die Stetigkeits- und Monotonieeigenschaft besitzt, die in der Definitionsgleichung (56) formuliert worden ist.
  
  $\Box$

Beispiele

 

1. $\;$ Normalverteilte Stichprobenvariablen (bei bekannter Varianz)
   • Sei $\sigma^2>0$ eine beliebige, jedoch vorgegebene Zahl, und sei $\{P_\theta,\theta\in\Theta\}=\{$N $(\mu,\sigma^2),\,\mu\in\mathbb{R}\}$.
   • Dann gilt
     

     $$L(x;\mu) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\Bigl(-\;\frac{(x-\mu)^2}{2\sigma^2}\Bigr)$$

     $$= \exp\Bigl(\frac{\mu x}{\sigma^2}\;-\;\frac{x^2}{2\sigma^2}\;-\;\frac{\mu^2}{ 2\sigma^2}\;-\;\log\sqrt{2\pi\sigma^2}\Bigr)$$

     $$= \exp\bigl(c(\mu)V(x)+d(\mu)+ U(x)\bigr)\,,$$

     
     
     wobei
     $$c(\mu)=\frac{\mu}{\sigma^2}\;,\quad d(\mu)=-\;\frac{\mu^2}{ 2 \s... ...\sqrt{2\pi\sigma^2}\,,\quad U(x)= -\;\frac{x^2}{2\sigma^2}\,,\quad V(x)=x\,.$$

   
   

2. $\;$ Bernoulli-verteilte Stichprobenvariablen
   • Sei $\{P_\theta,\theta\in\Theta\}=\{$Bin $(1,p),\,p\in(0,1)\}$.
   • Dann gilt $B=\{0,1\}$ und für jedes $x\in B$
     

     $$L(x;p) = p^x(1-p)^{1-x}$$

     $$= \exp\Bigl(x\log\Bigl(\frac{p}{1-p}\Bigr)+\log(1-p)\Bigr)$$

     $$= \exp\bigl(c(p)V(x)+d(p)+ U(x)\bigr)\,,$$

     
     
     wobei
     $$c(p)=\log\Bigl(\frac{p}{1-p}\Bigr)\,,\quad d(p)=\log(1-p)\,,\quad U(x)=0\,,\quad V(x)=x\,.$$

Beachte

 

• Für beide Beispiele ist $c:\Theta\to\mathbb{R}$ jeweils eine streng monoton wachsende Funktion.
• Aus Theorem 4.5 ergibt sich somit, daß $\{$N $(\mu,\sigma^2),\,\mu\in\mathbb{R}\}$ und $\{$Bin $(1,p),\,p\in(0,1)\}$ parametrische Verteilungsfamilien mit monotonem Likelihood-Quotient in $\widehat\theta(x_1,\ldots,x_n)=\overline x_n$ sind.