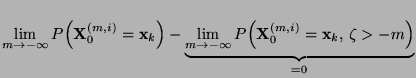- Bei der in Abschnitt 3.5.1 diskutierten
Vorwärtskopplung ist der Anfangspunkt 0 der Simulation deterministisch, wogegen der Endpunkt, d.h. der
Kopplungszeitpunkt
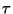 zufällig ist.
zufällig ist.
- Dabei stimmt die Zustandsverteilung der Markov-Kette
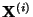 zum Kopplungszeitpunkt
zum Kopplungszeitpunkt 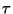 im allgemeinen nicht mit der
stationären Grenzverteilung
im allgemeinen nicht mit der
stationären Grenzverteilung
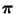 überein.
überein.
- das in der Literatur Coupling-from-the-Past (CFTP) bzw. Rückwärtskopplung genannt wird und
- das in der Mitte der 90-er Jahre von Propp und Wilson am Massachusetts Institute of Technology (MIT) entwickelt worden ist.
- Mit anderen Worten: Wir ,,starten'' die Markov-Ketten
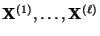 nicht zum ,,Zeitpunkt''
0,
nicht zum ,,Zeitpunkt''
0,
- sondern hinreichend weit in der ,,Vergangenheit'', so dass spätestens bis zum ,,Zeitpunkt'' 0 sämtliche Pfade miteinander verschmolzen sind.