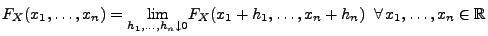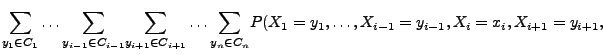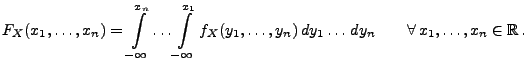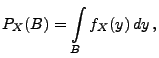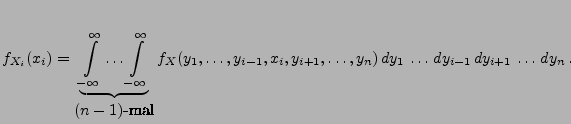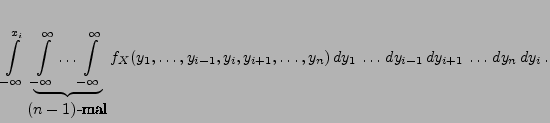- 1.
- Asymptotisches Verhalten im Unendlichen:
 Für beliebige
Für beliebige
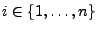 und
und
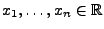 gilt
gilt
(i)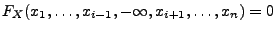 ,
wobei
(ii)
,
wobei
(ii)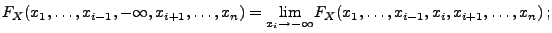
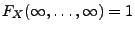 , wobei
, wobei
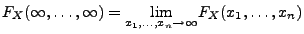 ;
;
(iii)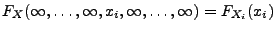 ,
wobei
,
wobei
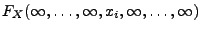 analog zu den in (i)-(ii) betrachteten Grenzwerten
definiert wird und
analog zu den in (i)-(ii) betrachteten Grenzwerten
definiert wird und
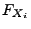 Randverteilungsfunktion von
Randverteilungsfunktion von  genannt wird.
genannt wird.
- 2.
- Monotonie:

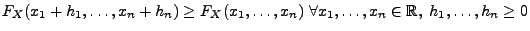
- 3.
- Rechtsstetigkeit: