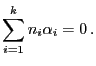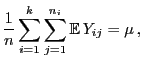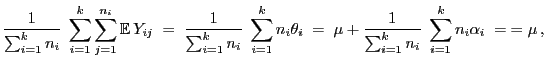- Dabei hat
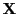 im ersten Fall vollen Rang, im zweiten Fall
jedoch keinen vollen Rang.
im ersten Fall vollen Rang, im zweiten Fall
jedoch keinen vollen Rang.
- Die zweite (reparametrisierte) Darstellung ist auf die Anwendung der allgemeinen Schätz- und Testverfahren ausgerichtet, die in den Abschnitten 3.2 und 3.3 behandelt werden.
- Bei normalverteilten Störgrößen lässt sich auf diese Weise unter
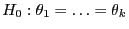 die Verteilung der in
(8) betrachteten Testgröße
die Verteilung der in
(8) betrachteten Testgröße
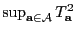 bestimmen, vgl. die Formel
(88) in Abshcnitt 3.4.1.
bestimmen, vgl. die Formel
(88) in Abshcnitt 3.4.1.