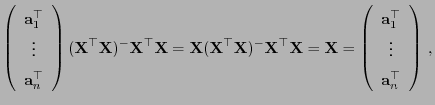Nächste Seite: Beste lineare erwartungstreue Schätzer;
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Erwartungswertvektor und Kovarianzmatrix des
Inhalt
Schätzbare Funktionen
- In Abschnitt 3.2.2 hatten wir gezeigt, dass es im
linearen Modell ohne Nebenbedingungen keinen erwartungstreuen
KQ-Schätzer für
 gibt, wenn die Designmatrix
gibt, wenn die Designmatrix
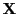 keinen vollen Rang besitzt.
keinen vollen Rang besitzt.
- Anstelle des Vektors
 betrachtet man deshalb eine Klasse
von (reellwertigen) linearen Funktionen
betrachtet man deshalb eine Klasse
von (reellwertigen) linearen Funktionen
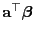 des
Parametervektors
des
Parametervektors
 , für die erwartungstreue KQ-Schätzer
konstruiert werden können.
, für die erwartungstreue KQ-Schätzer
konstruiert werden können.
- Mit anderen Worten: Anstelle der (vektoriellen)
Lineartransformation
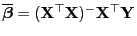 der
Zufallsstichprobe
der
Zufallsstichprobe
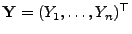 betrachtet man
eine Klasse von (reellwertigen) linearen Funktionen
betrachtet man
eine Klasse von (reellwertigen) linearen Funktionen
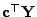 von
von
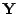 , die als Schätzer von
, die als Schätzer von
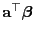 aufgefasst werden.
aufgefasst werden.
- Dies führt zu der folgenden Begriffsbildung.
- Definition
-
- Beispiel
 (einfaktorielle Varianzanalyse)
(einfaktorielle Varianzanalyse)
- Beispiel
 (zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)
(zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)
Das folgende Hilfsergebnis, das eine Ergänzung von
Lemma 3.5 ist, benötigen wir, um zwei allgemeine
Kriterien für die erwartungstreue Schätzbarkeit von linearen
Funktionen
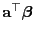 des Parametervektors
des Parametervektors
 herzuleiten.
herzuleiten.
Lemma 3.6

Sei
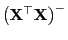
eine verallgemeinerte Inverse von
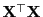
. Dann gilt
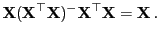 |
(45) |
- Beweis
 In Lemma 3.5 hatten wir gezeigt, dass
In Lemma 3.5 hatten wir gezeigt, dass
- die transponierte Matrix
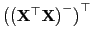 ebenfalls eine
verallgemeinerte Inverse von
ebenfalls eine
verallgemeinerte Inverse von
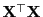 ist und dass
ist und dass
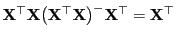 .
.
- Damit gilt auch
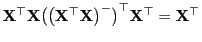 .
.
- Hieraus ergibt sich (45) durch Vertauschen von
Spalten und Zeilen.

Theorem 3.9

Sei
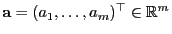
ein beliebiger Vektor.
Die lineare Funktion
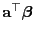
des Parametervektors

ist genau dann erwartungstreu schätzbar, wenn eine der
folgenden beiden Bedingungen erfüllt ist:
- 1.
- Es gibt ein
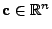 , so dass
, so dass
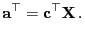 |
(46) |
- 2.
- Der Vektor
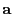 genügt dem folgenden Gleichungssystem:
genügt dem folgenden Gleichungssystem:
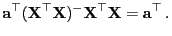 |
(47) |
- Beweis
-
- Beachte
-
- Wenn die Designmatrix
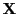 vollen Rang hat, d.h.
vollen Rang hat, d.h.
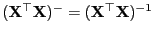 , dann ist die
Bedingung (47) offenbar für jedes
, dann ist die
Bedingung (47) offenbar für jedes
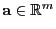 erfüllt.
erfüllt.
- In diesem Fall ist somit jede lineare Funktion des
Parametervektors
 erwartungstreu schätzbar, was bereits
in Theorem 2.2 gezeigt wurde.
erwartungstreu schätzbar, was bereits
in Theorem 2.2 gezeigt wurde.
Für den Fall, dass die Designmatrix
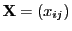 keinen vollen
Rang hat, zeigen wir,
keinen vollen
Rang hat, zeigen wir,
- Beweis
-




Nächste Seite: Beste lineare erwartungstreue Schätzer;
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Erwartungswertvektor und Kovarianzmatrix des
Inhalt
Hendrik Schmidt
2006-02-27
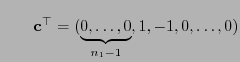
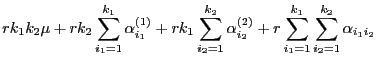
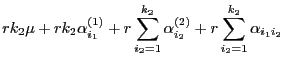
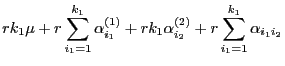
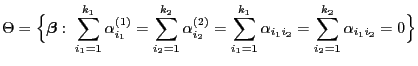
![]() des Parametervektors
des Parametervektors
![]() herzuleiten.
herzuleiten.
![]() keinen vollen
Rang hat, zeigen wir,
keinen vollen
Rang hat, zeigen wir,