



Nächste Seite: Normalverteilte Störgrößen
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Schätzbare Funktionen
Inhalt
Beste lineare erwartungstreue Schätzer; Gauß-Markow-Theorem
- In diesem Abschnitt zeigen wir, wie BLUE-Schätzer für schätzbare
Funktionen des Parametervektors
 konstruiert werden
können.
konstruiert werden
können.
- Zur Erinnerung: Ein linearer erwartungstreuer Schätzer wird
BLUE-Schätzer genannt, wenn es keinen linearen erwartungstreuen
Schätzer gibt, dessen Varianz kleiner ist (BLUE = best linear
unbiased estimator).
- In der Theorie linearer Modelle wird das folgende Resultat das
Gauß-Markow-Theorem genannt.
- Beweis
-
- Wir zeigen zuerst, dass
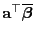 ein linearer
erwartungstreuer Schätzer für
ein linearer
erwartungstreuer Schätzer für
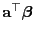 ist.
ist.
- Es ist klar, dass
eine lineare Funktion der Zufallsstichprobe
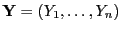 ist.
ist.
- Weil vorausgesetzt wird, dass
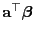 eine schätzbare
Funktion des Parametervektors
eine schätzbare
Funktion des Parametervektors
 ist, folgt aus
Theorem 3.9, dass es ein
ist, folgt aus
Theorem 3.9, dass es ein
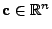 gibt, so
dass
gibt, so
dass
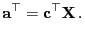 |
(51) |
- Somit gilt für jedes
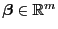 , dass
wobei sich die vorletzte Gleichheit aus Lemma 3.6
ergibt.
, dass
wobei sich die vorletzte Gleichheit aus Lemma 3.6
ergibt.
- Damit ist gezeigt, dass
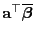 ein linearer
erwartungstreuer Schätzer für
ein linearer
erwartungstreuer Schätzer für
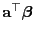 ist.
ist.
- Aus den Rechenregeln für die Varianz (vgl. Theorem WR-4.13) ergibt
sich, dass
- Außerdem hatten wir in Theorem 3.7 gezeigt, dass
- Hieraus folgt, dass
wobei sich die vorletzte Gleichheit aus (51) und
die letzte Gleichheit aus Lemma 3.5 ergibt.
- Die erneute Anwendung von (51) liefert die
Varianzformel (50).
- Es ist noch zu zeigen, dass der Schätzer
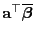 die kleinste Varianz in der Klasse
aller linearen erwartungstreuen Schätzer für
die kleinste Varianz in der Klasse
aller linearen erwartungstreuen Schätzer für
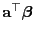 hat.
hat.
- Sei
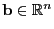 , so dass
, so dass
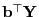 ein linearer
erwartungstreuer Schätzer für
ein linearer
erwartungstreuer Schätzer für
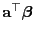 ist. Dann gilt
und somit auch
ist. Dann gilt
und somit auch
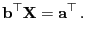 |
(52) |
- Für die Kovarianz von
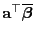 und
und
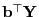 gilt
wobei sich die letzte Gleichheit aus (52) ergibt.
gilt
wobei sich die letzte Gleichheit aus (52) ergibt.
- Hieraus und aus der Varianzformel (50) folgt, dass

- Beachte
-
- Im Beweis von Theorem 3.11 wurde nirgendwo explizit
genutzt, dass
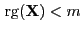 .
.
- Mit anderen Worten: Wenn die Designmatrix
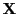 vollen Rang hat,
d.h.
vollen Rang hat,
d.h.
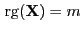 , dann ist
, dann ist
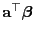 für jeden
für jeden
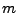 -dimensionalen Vektor
-dimensionalen Vektor
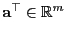 erwartungstreu
schätzbar, und
erwartungstreu
schätzbar, und
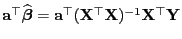 ist ein BLUE-Schätzer für
ist ein BLUE-Schätzer für
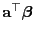 .
.
Aus der folgenden Invarianzeigenschaft der verallgemeinerten
Inversen
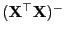 von
von
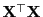 ergibt sich,
dass der in Theorem 3.11 betrachtete BLUE-Schätzer
ergibt sich,
dass der in Theorem 3.11 betrachtete BLUE-Schätzer
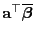 nicht von der spezifischen
Wahl von
nicht von der spezifischen
Wahl von
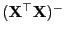 abhängt.
abhängt.
Lemma 3.7

Seien

und
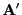
beliebige verallgemeinerte Inverse der Matrix
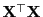
.
Dann gilt
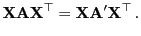 |
(53) |
- Beweis
-
Mit Hilfe von Lemma 3.7 kann nun die oben erwähnte
Invarianzeigenschaft des in Theorem 3.11 betrachteten
BLUE-Schätzers
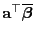 bewiesen werden.
bewiesen werden.
Theorem 3.12

Sei
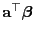
eine schätzbare Funktion des
Parametervektors

. Dann hängt der BLUE-Schätzer
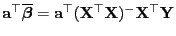
nicht von der Wahl der verallgemeinerten Inversen
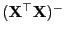
ab.
- Beweis
-
- Beispiel
 (einfaktorielle Varianzanalyse)
(einfaktorielle Varianzanalyse)
- Beispiel
 (zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)
(zweifaktorielle Varianzanalyse mit balancierten Teilstichproben)




Nächste Seite: Normalverteilte Störgrößen
Aufwärts: Schätzung der Modellparameter
Vorherige Seite: Schätzbare Funktionen
Inhalt
Hendrik Schmidt
2006-02-27
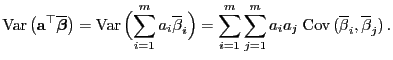
![]() von
von
![]() ergibt sich,
dass der in Theorem 3.11 betrachtete BLUE-Schätzer
ergibt sich,
dass der in Theorem 3.11 betrachtete BLUE-Schätzer
![]() nicht von der spezifischen
Wahl von
nicht von der spezifischen
Wahl von
![]() abhängt.
abhängt.
![]() bewiesen werden.
bewiesen werden.