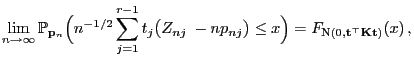Nächste Seite: -Anpassungstest von Pearson-Fisher
Aufwärts: -Anpassungstest
Vorherige Seite: Asymptotische Verteilung
Inhalt
Güteeigenschaften; lokale Alternativen
Es ist nicht schwierig, die folgende (punktweise) Konsistenz des
 --Anpassungstests zu zeigen.
--Anpassungstests zu zeigen.
Theorem 5.6

Der

--Anpassungstest ist punktweise konsistent gegen
jeden Vektor
![$ {\mathbf{p}}=(p_1,\ldots,p_{r-1})^\top\in[0,1]^{r-1}$](img2012.png)
mit
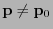
, d.h., es gilt
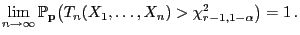 |
(43) |
- Beweis
-
- Beachte
-
Um diese Behauptung zu beweisen, benötigen wir als Hilfsmittel die
folgende Abschätzung, die in der Literatur die Ungleichung
von Berry-Esséen genannt wird.
Lemma 5.5

Sei
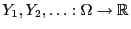
eine Folge von unabhängigen und
identisch verteilten Zufallsvariablen mit
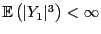
. Wenn
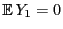
und
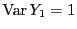
, dann gilt für jedes
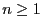
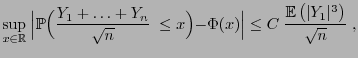 |
(47) |
wobei
![$ \Phi:\mathbb{R}\to[0,1]$](img2087.png)
die Verteilungsfunktion der
N
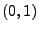
-Verteilung bezeichnet und
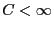
eine universelle
Konstante ist, die nicht von der Verteilung der Zufallsvariablen
abhängt.
Theorem 5.7

Sei
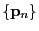
eine Folge von Vektoren, die durch
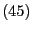
und
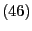
gegeben sind.
- Beweis
-
- Der Beweis der ersten Teilaussage verläuft analog zum Beweis von
Theorem 5.5, denn für den in (39)
eingeführten Zufallsvektor
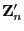 gilt wegen
(45) und (46), dass
gilt wegen
(45) und (46), dass
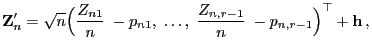 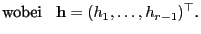 |
(51) |
- Wegen (51) kann man so wie beim Beweis des
multivariaten zentralen Grenzwertsatzes in
Lemma 5.2 zeigen, dass
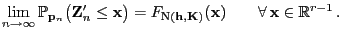 |
(52) |
- Dabei genügt es lediglich zu beachten, dass man mit der
Ungleichung von Berry-Esséen in Lemma 5.5 zeigen
kann, dass (in Analogie zu Formel (10) im Beweis
von Lemma 5.2)
- für beliebige
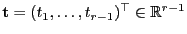 und
und
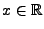
- wobei
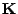 die in (41) eingeführte
Kovarianzmatrix ist.
die in (41) eingeführte
Kovarianzmatrix ist.
- Genauso wie im Beweis von Theorem 5.5 erhalten wir
nun aus (52), dass
- Hieraus und aus der Definition der nichtzentralen
 -Verteilung in Abschnitt 1.3.2 ergibt sich,
dass
-Verteilung in Abschnitt 1.3.2 ergibt sich,
dass
- wobei
 die inverse Matrix
die inverse Matrix
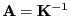 in
(42) ist und der Nichtzentralitätsparameter
in
(42) ist und der Nichtzentralitätsparameter
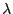 gegeben ist durch
gegeben ist durch
- Damit ist (48) bewiesen, und wegen
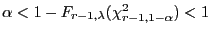 ergibt sich
hieraus auch die Gültigkeit von (50).
ergibt sich
hieraus auch die Gültigkeit von (50).





Nächste Seite: -Anpassungstest von Pearson-Fisher
Aufwärts: -Anpassungstest
Vorherige Seite: Asymptotische Verteilung
Inhalt
Hendrik Schmidt
2006-02-27
![]() --Anpassungstests zu zeigen.
--Anpassungstests zu zeigen.