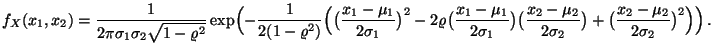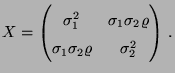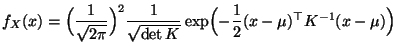Next: Abschätzungen und Grenzwertsätze
Up: Gemischte Momente
Previous: Linearer Zusammenhang von Zufallsvariablen
Contents
Erwartungswertvektor und Kovarianzmatrix
Wir zeigen zunächst, wie der Begriff der
Kovarianz genutzt werden kann, um das in Korollar 4.8 angegebene
Additionstheorem (20) für Varianzen zu verallgemeinern.
- Theorem 4.13
- Seien
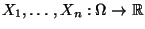 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
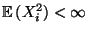 für
jedes
für
jedes
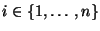 . Dann gilt
. Dann gilt
Falls die Zufallsvariablen
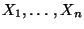 paarweise
unkorreliert sind, dann gilt insbesondere
paarweise
unkorreliert sind, dann gilt insbesondere
- Beweis
-
- Wir betrachten zunächst den Fall
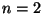 .
.
- Dann ergibt sich sofort aus dem Beweis von
Korollar 4.8, daß
- Für beliebiges
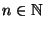 ergibt sich die Gültigkeit
von (31) nun mittels vollständiger
Induktion.
ergibt sich die Gültigkeit
von (31) nun mittels vollständiger
Induktion.
- Die Gleichung (32) ergibt sich
unmittelbar aus (28) und (31).
- Beachte
 Neben den Erwartungswerten
Neben den Erwartungswerten
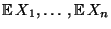 und den Varianzen
Var
und den Varianzen
Var 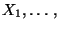 Var
Var 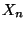 sind die in
(31) auftretenden Kovarianzen
sind die in
(31) auftretenden Kovarianzen
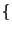 Cov
Cov 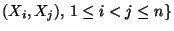 wichtige Charakteristiken des Zufallsvektors
wichtige Charakteristiken des Zufallsvektors
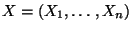 .
.
Dies führt zu den folgenden Begriffsbildungen.
- Definition 4.14
 Seien
Seien
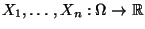 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
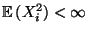 für
jedes
für
jedes
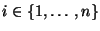 .
.
- Der Vektor
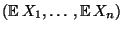 heißt
der Erwartungswertvektor des Zufallsvektors
heißt
der Erwartungswertvektor des Zufallsvektors
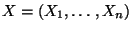 .
.
Schreibweise:
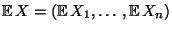
- Die
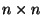 -Matrix
-Matrix
Cov
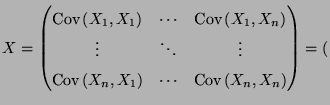
Cov
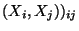
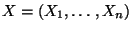 .
.
- Theorem 4.15
 Die Kovarianzmatrix
Cov
Die Kovarianzmatrix
Cov  ist
ist
- symmetrisch, d.h., für beliebige
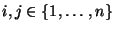 gilt
gilt
Cov 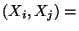 Cov Cov 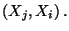 |
(33) |
- nichtnegativ definit, d.h., für jedes
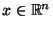 gilt
gilt
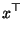 Cov Cov 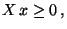 |
(34) |
wobei 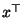 ist der zu
ist der zu 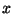 transponierte
Vektor ist.
transponierte
Vektor ist.
- Beweis
-
- Die Symmetrieeigenschaft (33) ergibt
sich unmittelbar aus der Definition 4.9 der Kovarianz.
- Die Ungleichung (34) ergibt sich durch
eine einfache Rechnung aus (15) und
aus der Definition 4.9 der Kovarianz.
- Beachte
 Die Matrix
Cov
Die Matrix
Cov  heißt positiv
definit, falls
heißt positiv
definit, falls
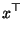 Cov Cov 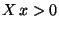 |
(35) |
für jedes
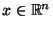 mit
mit 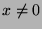 .
.
- Beispiel
 (zweidimensionale Normalverteilung)
(zweidimensionale Normalverteilung)
- Beachte
-
- Die Verteilung eines normalverteilten Zufallsvektors
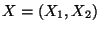 wird eindeutig durch den
Erwartungswertvektor
wird eindeutig durch den
Erwartungswertvektor
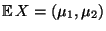 und die
Kovarianzmatrix
Cov
und die
Kovarianzmatrix
Cov  bestimmt.
Für beliebige (nicht normalverteilte)
Zufallsvektoren gilt diese Eindeutigkeitsaussage jedoch im
allgemeinen nicht.
bestimmt.
Für beliebige (nicht normalverteilte)
Zufallsvektoren gilt diese Eindeutigkeitsaussage jedoch im
allgemeinen nicht.
- Es gilt
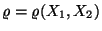 .
Außerdem ergibt sich aus (36), daß
.
Außerdem ergibt sich aus (36), daß
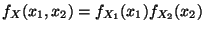 genau dann, wenn
genau dann, wenn 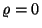 . Die Komponenten
. Die Komponenten 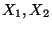 eines
normalverteilten Zufallsvektors
eines
normalverteilten Zufallsvektors
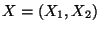 sind also
genau dann unabhängig, wenn sie unkorreliert sind.
sind also
genau dann unabhängig, wenn sie unkorreliert sind.
- Weil
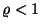 vorausgesetzt wird, ist die
Determinante der Kovarianzmatrix
Cov
vorausgesetzt wird, ist die
Determinante der Kovarianzmatrix
Cov  nicht Null,
d.h., die Matrix
Cov
nicht Null,
d.h., die Matrix
Cov  ist positiv definit und invertierbar.
Man kann sich deshalb leicht überlegen, daß die in (36)
gegebenen Dichte
ist positiv definit und invertierbar.
Man kann sich deshalb leicht überlegen, daß die in (36)
gegebenen Dichte 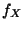 von
von  auch wie folgt dargestellt werden
kann: Es gilt
auch wie folgt dargestellt werden
kann: Es gilt
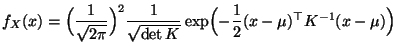 |
(38) |
für jedes
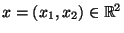 , wobei
, wobei
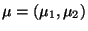 und
und 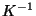 die inverse Matrix zu der in (37) gegebenen
Kovarianzmatrix
die inverse Matrix zu der in (37) gegebenen
Kovarianzmatrix
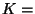 Cov
Cov  bezeichnet.
bezeichnet.
Schreibweise: 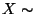 N
N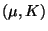 .
.
- Man kann sich leicht überlegen, daß die
Randverteilungen von
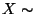 N
N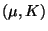 (eindimensionale)
Normalverteilungen sind mit
(eindimensionale)
Normalverteilungen sind mit 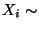 N
N
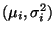 für
für 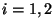 .
.
- Manchmal betrachtet man auch Zufallsvektoren
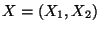 , deren Komponenten
, deren Komponenten 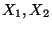 normalverteilt
sind mit
normalverteilt
sind mit
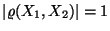 . Aus Theorem 4.12 folgt
dann, daß
. Aus Theorem 4.12 folgt
dann, daß
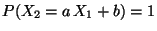 für ein Zahlenpaar
für ein Zahlenpaar
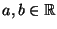 .
In diesem Fall ist der Zufallsvektor
.
In diesem Fall ist der Zufallsvektor
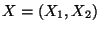 nicht absolutstetig, obwohl seine Komponenten diese
Eigenschaft besitzen.
nicht absolutstetig, obwohl seine Komponenten diese
Eigenschaft besitzen.
Für Zufallsvektoren mit einer beliebigen Dimension
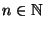 kann man
den Begriff der
kann man
den Begriff der  -dimensionalen Normalverteilung einführen, indem
man eine zu
(38) analoge Dichte-Formel betrachtet.
-dimensionalen Normalverteilung einführen, indem
man eine zu
(38) analoge Dichte-Formel betrachtet.
- Definition 4.16
-




Next: Abschätzungen und Grenzwertsätze
Up: Gemischte Momente
Previous: Linearer Zusammenhang von Zufallsvariablen
Contents
Roland Maier
2001-08-20
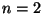 .
.
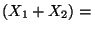 Var
Var 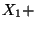 Var
Var 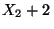 Cov
Cov 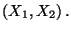
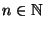 ergibt sich die Gültigkeit
von (31) nun mittels vollständiger
Induktion.
ergibt sich die Gültigkeit
von (31) nun mittels vollständiger
Induktion.
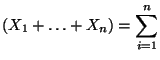 Var
Var 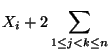 Cov
Cov 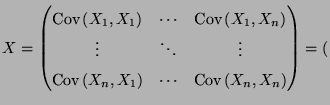 Cov
Cov