



Next: Momentenmethode
Up: Schätzung von Parametern
Previous: Schätzung von Parametern
Contents
Eigenschaften von Parameterschätzern
- Betrachten eine beliebige (Borel-meßbare) Stichprobenfunktion
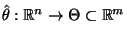
- und den zugehörigen Schätzer
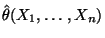 des
Parametervektors
des
Parametervektors 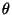 .
.
- Definition 5.13
-
- Es gelte
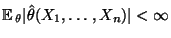 für
jedes
für
jedes
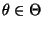 , wobei
, wobei
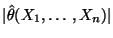 die
Länge des Zufallsvektors
die
Länge des Zufallsvektors
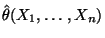 bezeichnet.
bezeichnet.
- Dann heißt der Schätzer
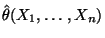
- erwartungstreu, falls
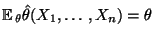 für jedes
für jedes
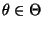 ,
,
- asymptotisch erwartungstreu, falls
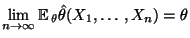 für
jedes
für
jedes
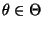 .
.
- Beachte
 Die folgende Sprechweise ist üblich:
Die folgende Sprechweise ist üblich:
- Die Differenz
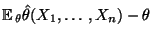 heißt
Verzerrung (Synonym: Bias).
heißt
Verzerrung (Synonym: Bias).
- Falls
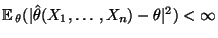 ,
dann heißt
,
dann heißt
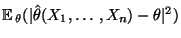 die erwartete quadratische Abweichung des Schätzers
die erwartete quadratische Abweichung des Schätzers
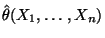 von dem zu schätzenden
Parametervektor
von dem zu schätzenden
Parametervektor
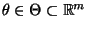 .
.
- Beispiel
-
- Die Stichprobenvariablen
 seien normalverteilt, d.h., es
gelte (26).
seien normalverteilt, d.h., es
gelte (26).
- Dann ist
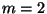 .
.
- Aus (3) und (10) ergibt sich, daß
der in (2) bzw. (9) eingeführte
Schätzer
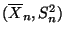 des Parametervektors
des Parametervektors
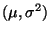 erwartungstreu ist.
erwartungstreu ist.
- Definition 5.14
 Der Schätzer
Der Schätzer
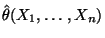 des Parametervektors
des Parametervektors
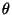 heißt
heißt
- schwach konsistent, falls für
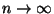 d.h.
für jedes
d.h.
für jedes
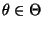 .
.
- stark konsistent, falls für
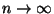 d.h.
für jedes
d.h.
für jedes
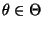 .
.
- Beispiel
-
- Die Stichprobenvariablen
 seien normalverteilt, d.h., es
gelte (26).
seien normalverteilt, d.h., es
gelte (26).
- Dann ergibt sich aus (5) und (12),
daß der in (2) bzw. (9) eingeführte
Schätzer
des Parametervektors
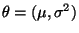 sowohl schwach als
auch stark konsistent ist.
sowohl schwach als
auch stark konsistent ist.
Schließlich wollen wir noch den Begriff der asymptotischen
Normalverteiltheit von Schätzern erwähnen. Hierfür benötigen wir
einen Hilfssatz aus der linearen Algebra, auf dessen Herleitung
wir jedoch im Rahmen dieser Vorlesung nicht eingehen.
- Lemma 5.15
 Sei
Sei 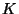 eine symmetrische und positiv
definite
eine symmetrische und positiv
definite 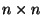 -Matrix. Dann gibt es eine eindeutig
bestimmte symmetrische und positiv definite
-Matrix. Dann gibt es eine eindeutig
bestimmte symmetrische und positiv definite 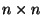 -Matrix
-Matrix
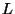 , so daß
, so daß
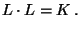 |
(27) |
- Beachte
-
- Die in (27) definierte Matrix
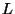 heißt Quadratwurzel von
heißt Quadratwurzel von 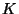 . (Schreibweise:
. (Schreibweise: 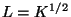 )
)
- Die Quadratwurzel der inversen Matrix
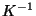 wird mit
wird mit 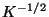 bezeichnet.
bezeichnet.
- Definition 5.16
 Die Kovarianzmatrix
Cov
Die Kovarianzmatrix
Cov 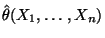 des
Schätzers
des
Schätzers
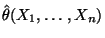 sei für jedes
sei für jedes
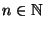 und
für jedes
und
für jedes
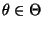 positiv definit. Dann heißt der
Schätzer
positiv definit. Dann heißt der
Schätzer
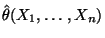 des Parametervektors
des Parametervektors
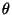 asymptotisch normalverteilt, falls
asymptotisch normalverteilt, falls
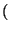
Cov
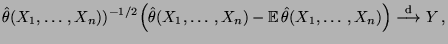
wobei 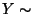 N
N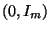 und
und 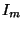 die
die 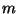 -dimensionale
Einheitsmatrix bezeichnet.
-dimensionale
Einheitsmatrix bezeichnet.




Next: Momentenmethode
Up: Schätzung von Parametern
Previous: Schätzung von Parametern
Contents
Roland Maier
2001-08-20