So wie in Abschnitt 5.3.5 nehmen wir nun an, daß die
Stichprobenvariablen
![]() (zweidimensionale)
normalverteilte Zufallsvektoren sind mit
(zweidimensionale)
normalverteilte Zufallsvektoren sind mit
![]() .
Dabei setzen wir zunächst voraus, daß die Komponenten
.
Dabei setzen wir zunächst voraus, daß die Komponenten ![]() und
und
![]() von
von ![]() unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
unabhängige (jedoch im allgemeinen nicht
identisch verteilte) Zufallsvariable sind.
Für zwei beliebige, jedoch vorgegebene Zahlen
![]() betrachten wir also zwei unabhängige Zufallsstichproben
betrachten wir also zwei unabhängige Zufallsstichproben
![]() und
und
![]() , wobei
wir
, wobei
wir
Wir diskutieren in diesem Abschnitt nur Beispiele von zweiseitigen
Tests. Wie in Abschnitt 5.4.2 gezeigt wurde, lassen sich
dann leicht die entsprechenden einseitigen Tests konstruieren.
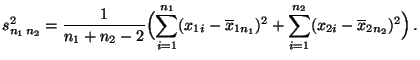
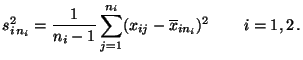
Wir testen nun die Gleichheit zweier Erwartungswerte bei
verbundenen Stichproben, vgl. das letzte Beispiel in
Abschnitt 5.3.5.
Dabei setzen wir voraus, daß ![]()
![]() . Die
Zufallstichproben
. Die
Zufallstichproben
![]() und
und
![]() müssen jedoch jetzt nicht
unabhängig sein.
müssen jedoch jetzt nicht
unabhängig sein.
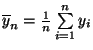 und
und
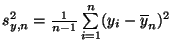 .
.