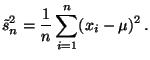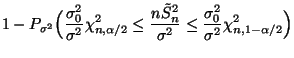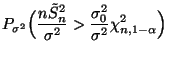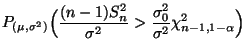Next: Zwei-Stichproben-Tests
Up: Tests statistischer Hypothesen
Previous: Kritischer Bereich; Fehlerwahrscheinlichkeiten
Contents
Parametertests bei Normalverteilung
Wir nehmen in diesem Abschnitt an, daß die Stichprobenvariablen
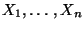 normalverteilt sind, d.h., es gelte
normalverteilt sind, d.h., es gelte
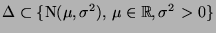 .
Wir betrachten also die Familie der (eindimensionalen)
Normalverteilungen bzw. Teilmengen hiervon.
.
Wir betrachten also die Familie der (eindimensionalen)
Normalverteilungen bzw. Teilmengen hiervon.
Wir konstruieren zunächst Tests für den Erwartungswert 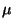 .
Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für
.
Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für 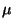 , die in Abschnitt 5.3.4
diskutiert werden.
, die in Abschnitt 5.3.4
diskutiert werden.
- Beispiel
 Test des Erwartungswertes
Test des Erwartungswertes 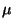 (bei bekannter Varianz
(bei bekannter Varianz
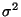 )
)
Für
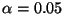 und
und
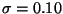 wollen wir nun prüfen, ob
wollen wir nun prüfen, ob
- die Hypothese
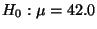 mit der bereits in
Abschnitt 5.3.2 betrachteten (konkreten) Stichprobe
vereinbar ist.
mit der bereits in
Abschnitt 5.3.2 betrachteten (konkreten) Stichprobe
vereinbar ist.
- In diesem Fall gilt
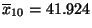 , und aus
(76) ergibt sich somit
, und aus
(76) ergibt sich somit
wobei das Quantil
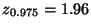 aus Tabelle 1 entnommen wurde.
aus Tabelle 1 entnommen wurde.
- Die Hypothese
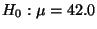 wird also verworfen.
wird also verworfen.
- Beachte
-
- Man kann sich leicht überlegen, daß
- Falls die Hypothese
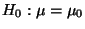 gegen die (einseitige)
Alternative
gegen die (einseitige)
Alternative
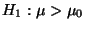 getestet werden soll, d.h.
getestet werden soll, d.h.
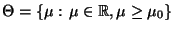 mit
mit
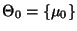
bzw.
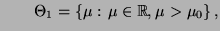
dann könnte man zwar so wie bisher vorgehen und für die in
(76) definierte Testgröße 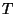
- den kritischen Bereich
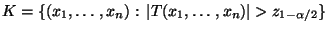 betrachten.
betrachten.
- Ein besserer Test ergibt sich jedoch, wenn der folgende
(einseitige) kritische Bereich
betrachtet wird, denn für jedes
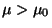 gilt
gilt
- Falls die Hypothese
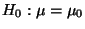 gegen die Alternative
gegen die Alternative
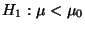 getestet werden soll, dann wird der kritische
Bereich
getestet werden soll, dann wird der kritische
Bereich
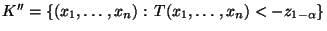 betrachtet.
betrachtet.
Wir diskutieren nun einen Test des Erwartungswertes 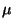 , wobei
angenommen wird, daß die Varianz
, wobei
angenommen wird, daß die Varianz 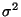 ebenfalls unbekannt
ist.
ebenfalls unbekannt
ist.
- Beispiel
 Test des Erwartungswertes
Test des Erwartungswertes 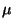 (bei unbekannter Varianz
(bei unbekannter Varianz
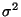 )
)
Für
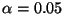 wollen wir nun prüfen, ob
wollen wir nun prüfen, ob
- Beachte
-
- Falls die Hypothese
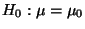 gegen die Alternative
gegen die Alternative
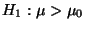 getestet werden soll, dann wird (ähnlich wie in
dem vorhergehenden Beispiel) für die in (77)
definierte Testgröße
getestet werden soll, dann wird (ähnlich wie in
dem vorhergehenden Beispiel) für die in (77)
definierte Testgröße 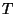 der kritische Bereich
der kritische Bereich 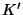 betrachtet mit
betrachtet mit
- Analog wird für den Test der Hypothese
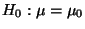 gegen die
Alternative
gegen die
Alternative
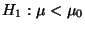 der kritische Bereich
der kritische Bereich
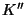 betrachtet mit
betrachtet mit
Wenn die Varianz 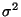 der normalverteilten
Stichprobenvariablen
der normalverteilten
Stichprobenvariablen
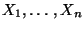 getestet werden soll, dann
kann man ähnlich wie in den beiden vorhergehenden Beispielen
argumentieren. Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für
getestet werden soll, dann
kann man ähnlich wie in den beiden vorhergehenden Beispielen
argumentieren. Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für 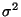 , die in
Abschnitt 5.3.4 diskutiert werden.
, die in
Abschnitt 5.3.4 diskutiert werden.
- Beispiel
 Test der Varianz
Test der Varianz 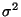 (bei bekanntem Erwartungswert
(bei bekanntem Erwartungswert
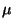 )
)
- Beachte
-
- Die Gütefunktion
![$ \alpha_n:\Theta\to[0,1]$](img1669.png) dieses Tests mit
dieses Tests mit
hat kein Minimum im Punkt
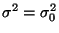 . Der Test ist also
nicht unverfälscht.
. Der Test ist also
nicht unverfälscht.
- Wenn jedoch beispielsweise die Hypothese
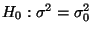 gegen die (einseitige) Alternative
gegen die (einseitige) Alternative
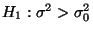 getestet werden soll, d.h.
getestet werden soll, d.h.
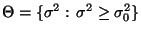 mit
mit
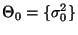
bzw.
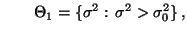
dann wird der kritische Bereich
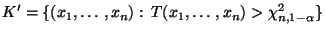 |
(79) |
betrachtet, und die Gütefunktion
![$ \alpha_n:\Theta\to[0,1]$](img1669.png) mit
mit
ist monoton wachsend für
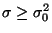 . Der einseitige
Test ist somit unverfälscht.
. Der einseitige
Test ist somit unverfälscht.
- Wegen dieser Monotonieeigenschaft ist durch den in (79)
betrachteten kritischen Bereich
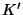 auch ein
(unverfälschter) Test zum Niveau
auch ein
(unverfälschter) Test zum Niveau 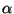 der Hypothese
der Hypothese
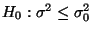 gegen die Alternativhypothese
gegen die Alternativhypothese
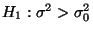 gegeben.
gegeben.
- Analog liefert der kritische Bereich
einen (unverfälschten) Test zum Niveau
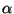 der Hypothesen
der Hypothesen
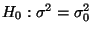 bzw.
bzw.
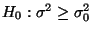 gegen
die Alternativhypothese
gegen
die Alternativhypothese
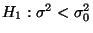 .
.
- Beispiel
 Test der Varianz
Test der Varianz 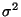 (bei unbekanntem Erwartungswert
(bei unbekanntem Erwartungswert
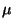 )
)
- Beachte
-
- Die Gütefunktion
![$ \alpha_n:\Theta\to[0,1]$](img1669.png) dieses Tests mit
hängt nicht von
dieses Tests mit
hängt nicht von 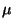 ab und hat (bei fixiertem
ab und hat (bei fixiertem 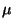 ) kein
Minimum im Punkt
) kein
Minimum im Punkt
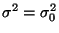 . Der Test ist also nicht unverfälscht.
. Der Test ist also nicht unverfälscht.
- Wenn jedoch beispielsweise die Hypothese
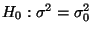 gegen die (einseitige) Alternative
gegen die (einseitige) Alternative
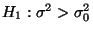 getestet werden soll, d.h.
getestet werden soll, d.h.
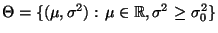 mit
mit
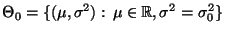
bzw.
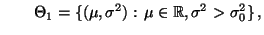
dann wird der kritische Bereich
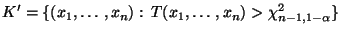 |
(81) |
betrachtet, und die Gütefunktion
![$ \alpha_n:\Theta\to[0,1]$](img1669.png) mit
mit
hängt nicht von 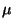 ab und ist monoton wachsend für
ab und ist monoton wachsend für
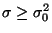 . Der einseitige Test ist somit unverfälscht.
. Der einseitige Test ist somit unverfälscht.
- Wegen dieser Monotonieeigenschaft ist durch den in
(81) betrachteten kritischen Bereich
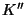 auch ein (unverfälschter) Test zum Niveau
auch ein (unverfälschter) Test zum Niveau
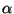 der Hypothese
der Hypothese
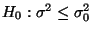 gegen die
Alternativhypothese
gegen die
Alternativhypothese
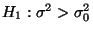 gegeben.
gegeben.
- Analog liefert der kritische Bereich
einen (unverfälschten) Test zum Niveau
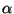 der Hypothesen
der Hypothesen
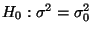 bzw.
bzw.
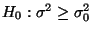 gegen
die Alternativhypothese
gegen
die Alternativhypothese
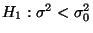 .
.




Next: Zwei-Stichproben-Tests
Up: Tests statistischer Hypothesen
Previous: Kritischer Bereich; Fehlerwahrscheinlichkeiten
Contents
Roland Maier
2001-08-20
![]() normalverteilt sind, d.h., es gelte
normalverteilt sind, d.h., es gelte
![]() .
Wir betrachten also die Familie der (eindimensionalen)
Normalverteilungen bzw. Teilmengen hiervon.
.
Wir betrachten also die Familie der (eindimensionalen)
Normalverteilungen bzw. Teilmengen hiervon.
![]() .
Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für
.
Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für ![]() , die in Abschnitt 5.3.4
diskutiert werden.
, die in Abschnitt 5.3.4
diskutiert werden.
![]() und
und
![]() wollen wir nun prüfen, ob
wollen wir nun prüfen, ob
![]() , wobei
angenommen wird, daß die Varianz
, wobei
angenommen wird, daß die Varianz ![]() ebenfalls unbekannt
ist.
ebenfalls unbekannt
ist.
![]() wollen wir nun prüfen, ob
wollen wir nun prüfen, ob
![]() der normalverteilten
Stichprobenvariablen
der normalverteilten
Stichprobenvariablen
![]() getestet werden soll, dann
kann man ähnlich wie in den beiden vorhergehenden Beispielen
argumentieren. Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für
getestet werden soll, dann
kann man ähnlich wie in den beiden vorhergehenden Beispielen
argumentieren. Dabei gibt es Ähnlichkeiten zur Konstruktion der
Konfidenzintervalle für ![]() , die in
Abschnitt 5.3.4 diskutiert werden.
, die in
Abschnitt 5.3.4 diskutiert werden.