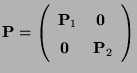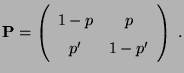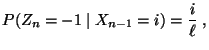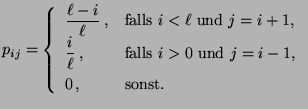Nächste Seite: Stationäre Anfangsverteilungen
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit; Perron-Frobenius-Theorem
Inhalt
Irreduzibilität und Aperiodizität
- Zur Erinnerung
- In Theorem 2.4 hatten wir die Ergodizität der
Markov-Kette
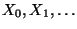 durch die Quasi-Positivität ihrer
Übergangsmatrix
durch die Quasi-Positivität ihrer
Übergangsmatrix
 charakterisiert.
charakterisiert.
- Es kann sich jedoch als schwierig erweisen, diese Eigenschaft von
 direkt nachzuweisen (insbesondere dann, wenn
direkt nachzuweisen (insbesondere dann, wenn 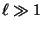 ).
).
- Wir leiten deshalb noch eine andere (probabilistische)
Charakterisierung der Ergodizität von Markov-Ketten mit endlichem
Zustandsraum her. Dabei benötigen wir den folgenden Begriff.
- Für beliebige, jedoch fest vorgegebene Zustände
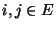 sagen
wir, dass der Zustand
sagen
wir, dass der Zustand 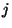 vom Zustand
vom Zustand 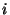 erreichbar ist,
falls
erreichbar ist,
falls
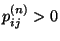 für ein
für ein 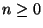 gilt, wobei
gilt, wobei
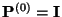 . (Schreibweise:
. (Schreibweise: 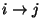 )
)
- Eine andere (äquivalente) Definitionsmöglichkeit der
Erreichbarbeit von Zuständen ist folgendermaßen gegeben.
- Hierfür sei
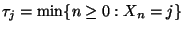 die Anzahl der Schritte
bis die Markov-Kette
die Anzahl der Schritte
bis die Markov-Kette 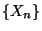 zum ersten Mal den Zustand
zum ersten Mal den Zustand 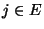 erreicht. Dabei setzen wir
erreicht. Dabei setzen wir
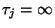 , falls
, falls 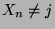 für
jedes
für
jedes 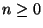 .
.
Theorem 2.7

Sei
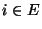
so gewählt, dass
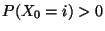
. In diesem Fall ist der
Zustand
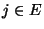
genau dann von
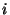
erreichbar, wenn
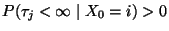
.
- Beweis
-
- Beachte
-
- Die Eigenschaft der Erreichbarkeit ist
- transitiv, d.h., aus
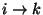 und
und 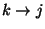 folgt
folgt 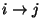 .
.
- Dies ergibt sich unmittelbar aus der Ungleichung
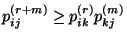 (vgl.
Korollar 2.2) und aus der Definition der
Erreichbarkeit.
(vgl.
Korollar 2.2) und aus der Definition der
Erreichbarkeit.
- Falls darüber hinaus
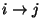 und
und 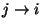 , dann sagen wir, dass
die Zustände
, dann sagen wir, dass
die Zustände 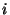 und
und 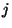 kommunizieren. (Schreibweise:
kommunizieren. (Schreibweise:
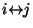 )
)
- Die Eigenschaft des Kommunizierens ist eine Äquivalenzrelation, denn es gilt
- (a)
-
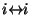 (Reflexivität),
(Reflexivität),
- (b)
-
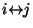 genau dann, wenn
genau dann, wenn
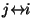 (Symmetrie),
(Symmetrie),
- (c)
-
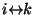 und
und
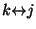 implizieren, dass
implizieren, dass
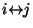 (Transitivität).
(Transitivität).
- Dies bedeutet insbesondere,
- dass der Zustandsraum
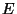 in (disjunkte und ausschöpfende)
Äquivalenzklassen bezüglich der Äquivalenzrelation
in (disjunkte und ausschöpfende)
Äquivalenzklassen bezüglich der Äquivalenzrelation
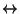 zerlegt werden kann.
zerlegt werden kann.
- Dabei heißt die Markov-Kette
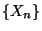 bzw. ihre Übergangsmatrix
bzw. ihre Übergangsmatrix
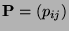 irreduzibel, wenn der Zustandsraum
irreduzibel, wenn der Zustandsraum 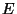 nur
aus einer solchen Äquivalenzklasse besteht, d.h., wenn
nur
aus einer solchen Äquivalenzklasse besteht, d.h., wenn
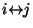 für sämtliche
für sämtliche 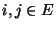 gilt.
gilt.
- Beispiele
-
- Unmittelbar aus der Definition der Irreduzibilität ergibt sich,
dass die
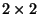 Matrizen
Matrizen
![$\displaystyle {\mathbf{P}}_1=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/2 & 1/2
\end{array}\right)$](img425.png)
und
![$\displaystyle \qquad
{\mathbf{P}}_2=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/4 & 3/4
\end{array}\right)
$](img426.png)
irreduzibel sind.
- Die aus
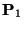 und
und
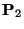 gebildete
gebildete 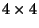 Matrix
Matrix
 mit der folgenden Blockstruktur
ist jedoch nicht irreduzibel.
mit der folgenden Blockstruktur
ist jedoch nicht irreduzibel.
Neben der Irreduzibilität benötigen wir noch eine weitere
Eigenschaft der Zustände, nämlich die sogenannte Aperiodizität, um die Ergodizität von Markov-Ketten auf
einfache Weise charakterisieren zu können.
- Definition
-
- Die Periode
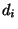 des Zustandes
des Zustandes 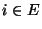 ist gegeben durch
ist gegeben durch
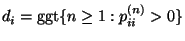 , wobei ,,ggt'' den
größten gemeinsamen Teiler bezeichnet. Dabei setzen wir
, wobei ,,ggt'' den
größten gemeinsamen Teiler bezeichnet. Dabei setzen wir
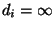 , falls
, falls
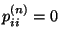 für jedes
für jedes 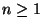 .
.
- Der Zustand
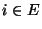 heißt aperiodisch, falls
heißt aperiodisch, falls 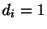 .
.
- Die Markov-Kette
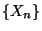 bzw. ihre Übergangsmatrix
bzw. ihre Übergangsmatrix
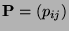 heißt aperiodisch, wenn sämtliche Zustände
von
heißt aperiodisch, wenn sämtliche Zustände
von 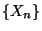 aperiodisch sind.
aperiodisch sind.
Wir zeigen nun, dass die Perioden 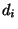 und
und 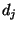 übereinstimmen,
wenn die Zustände
übereinstimmen,
wenn die Zustände 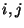 zu einundderselben Äquivalenzklasse von
kommunizierenden Zuständen gehören. Dabei verwenden wir die
Schreibweise
zu einundderselben Äquivalenzklasse von
kommunizierenden Zuständen gehören. Dabei verwenden wir die
Schreibweise ![$ i\to j[n]$](img438.png) , falls
, falls
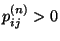 .
.
Theorem 2.8
Falls die Zustände
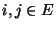
kommunizieren, dann gilt
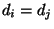
.
- Beweis
-
- Falls
![$ j\to j[n]$](img440.png) ,
, ![$ i\to j[k]$](img441.png) und
und ![$ j\to i[m]$](img442.png) for gewisse
for gewisse
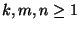 gilt, dann ergibt sich aus den Ungleichungen in
Korollar 2.2, dass
gilt, dann ergibt sich aus den Ungleichungen in
Korollar 2.2, dass
![$ i\to i[k+m]$](img444.png) und
und
![$ i\to i[k+m+n]$](img445.png) .
.
- Dies bedeutet, dass die natürlichen Zahlen
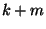 and
and 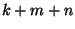 durch
durch
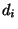 teilbar sind.
teilbar sind.
- Dann ist auch
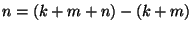 durch
durch 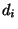 teilbar.
teilbar.
- Somit ist
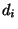 ein gemeinsamer Teiler für diejenigen natürlichen
Zahlen
ein gemeinsamer Teiler für diejenigen natürlichen
Zahlen 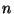 , für die
, für die
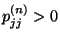 gilt, d.h.
gilt, d.h.
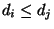 .
.
- Auf die gleiche Weise ergibt sich (aus Symmetriegründen), dass
auch
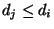 gilt.
gilt.

Korollar 2.5

Die Markov-Kette
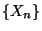
sei
irreduzibel. Dann besitzen sämtliche Zustände von
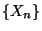
die
gleiche Periode.
Um zeigen zu können,
- dass die in Abschnitt 2.2.1 betrachtete
Charakterisierung (vgl. Theorem 2.4) der
Ergodizität von Markov-Ketten gleichbedeutend mit ihrer
Irreduzibilität und Aperiodizität ist,
- benötigen wir noch den folgenden elementaren Hilfssatz aus der
Zahlentheorie.
Lemma 2.3
Sei
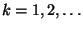
eine beliebige, jedoch fest vorgegebene
natürliche Zahl. Dann gibt es eine natürliche Zahl
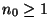
, so
dass
- Beweis
-
Theorem 2.9

Die Übergangsmatrix

ist genau dann quasi-positiv, wenn

irreduzibel und aperiodisch ist.
- Beweis
-
- Wir nehmen zunächst an, dass die Übergangsmatrix
 irreduzibel und aperiodisch ist.
irreduzibel und aperiodisch ist.
- Für jedes
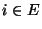 betrachten wir die Menge
betrachten wir die Menge
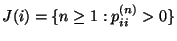 , deren größter gemeinsamer Teiler wegen der
Aperiodizität von
, deren größter gemeinsamer Teiler wegen der
Aperiodizität von
 gleich
gleich 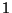 ist.
ist.
- Aus den Ungleichungen in Korollar 2.2 ergibt sich, dass
und somit
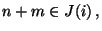 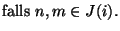 |
(50) |
- Wir zeigen, dass die Menge
 zwei aufeinanderfolgende Zahlen
enthält.
zwei aufeinanderfolgende Zahlen
enthält.
- Falls umgekehrt
 nicht zwei aufeinanderfolgende Zahlen
enthalten würde, dann würde es einen Minimalabstand
nicht zwei aufeinanderfolgende Zahlen
enthalten würde, dann würde es einen Minimalabstand 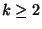 zwischen den Zahlen in
zwischen den Zahlen in  geben.
geben.
- Hieraus würde die Gültigkeit von
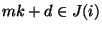 für gewisse
für gewisse
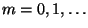 und
und
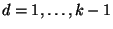 folgen, weil ansonsten
folgen, weil ansonsten 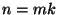 für alle
für alle 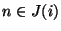 gelten würde.
gelten würde.
- Dies würde jedoch ein Widerspruch zu unserer Annahme sein, dass
ggt
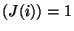 .
.
- Sei nun
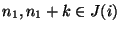 . Wegen (50) gilt dann
auch
. Wegen (50) gilt dann
auch
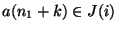 und
und
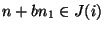 für beliebige
für beliebige
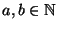 , wobei
, wobei
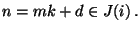 |
(51) |
- Wir zeigen jedoch,
- dass es dann natürliche Zahlen
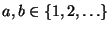 gibt, so
dass die Differenz zwischen
gibt, so
dass die Differenz zwischen
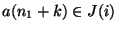 und
und
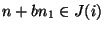 kleiner als
kleiner als 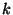 ist.
ist.
- Und zwar ergibt sich aus (51), dass
und somit für
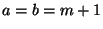
- Deshalb enthält die Menge
 zwei aufeinanderfolgende Zahlen.
zwei aufeinanderfolgende Zahlen.
- Aus (50) und aus Lemma 2.3 ergibt sich
nun, dass es für jedes
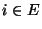 ein
ein 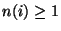 gibt, so dass
gibt, so dass
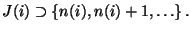 |
(52) |
- Hieraus, aus der Irreduzibilität von
 und aus der
Ungleichung (25) in Korollar 2.2, d.h.,
folgt, dass es für jedes Paar
und aus der
Ungleichung (25) in Korollar 2.2, d.h.,
folgt, dass es für jedes Paar 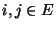 von Zuständen eine
natürliche Zahl
von Zuständen eine
natürliche Zahl
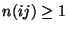 gibt, so dass
d.h.,
gibt, so dass
d.h.,
 ist quasi-positiv.
ist quasi-positiv.
- Umgekehrt ergibt sich die Irreduzibilität und Aperiodizität von
quasi-positiven Übergangsmatrizen unmittelbar aus den Definitionen
dieser Begriffe.

- Beachte
-
- Ein einfaches Beispiel einer Markov-Kette, die nicht
irreduzibel ist,
- kann durch das bereits mehrfach betrachtete Modell der Wettervorhersage gegeben werden, wobei
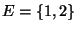 und
und
- Falls
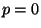 oder
oder
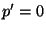 , dann ist die zugehörige
Markov-Kette offenbar nicht irreduzibel (und damit wegen
Theorem 2.9 auch nicht ergodisch).
, dann ist die zugehörige
Markov-Kette offenbar nicht irreduzibel (und damit wegen
Theorem 2.9 auch nicht ergodisch).
- Es ist dennoch möglich, dass das lineare Gleichungssystem
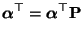 |
(53) |
eine (oder unendlich viele)
Wahrscheinlichkeitslösungen
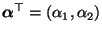 besitzt.
besitzt.
- Wenn beispielsweise
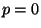 und
und
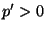 gilt, dann ist
gilt, dann ist 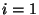 ein sogenannter absorbierender Zustand, und
ein sogenannter absorbierender Zustand, und
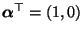 ist die (eindeutig bestimmte) Lösung des
linearen Gleichungssystems (53).
ist die (eindeutig bestimmte) Lösung des
linearen Gleichungssystems (53).
- Wenn
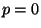 und
und
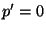 , dann ist jede
Wahrscheinlichkeitsfunktion
, dann ist jede
Wahrscheinlichkeitsfunktion
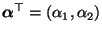 Lösung des linearen Gleichungssystems (53).
Lösung des linearen Gleichungssystems (53).
- Wir geben nun noch Beispiele von Markov-Ketten
 an, die nicht aperiodisch sind.
an, die nicht aperiodisch sind.
- Dabei sind die Zufallsvariablen
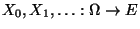 nicht durch eine stochastische Rekursionsgleichung
nicht durch eine stochastische Rekursionsgleichung
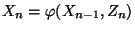 der Form (14) gegeben,
so dass die ,,Zuwächse''
der Form (14) gegeben,
so dass die ,,Zuwächse''
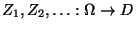 unabhängige
und identisch verteilte Zufallsvariablen sind.
unabhängige
und identisch verteilte Zufallsvariablen sind.
- Wir setzen nämlich lediglich voraus, dass die Zufallsvariablen
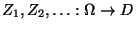 in dem folgenden Sinne ,,bedingt
unabhängig'' sind.
in dem folgenden Sinne ,,bedingt
unabhängig'' sind.
- Wie in Abschnitt 2.1.3 gezeigt wurde, kann man jedoch
stets eine zu
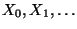 stochastisch äquivalente
Markov-Kette konstruieren, deren Zuwächse unabhängig sind, vgl.
das in (17)-(19) betrachtete
Konstruktionsprinzip.
stochastisch äquivalente
Markov-Kette konstruieren, deren Zuwächse unabhängig sind, vgl.
das in (17)-(19) betrachtete
Konstruktionsprinzip.
- Seien also
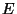 und
und 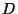 beliebige endliche (oder abzählbar
unendliche) Mengen, sei
beliebige endliche (oder abzählbar
unendliche) Mengen, sei
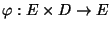 eine beliebige
Funktion, und seien
eine beliebige
Funktion, und seien
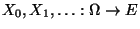 bzw.
bzw.
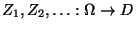 Zufallsvariablen,
Zufallsvariablen,
- Man kann zeigen (vgl. Übungsaufgabe 4.2), dass die durch
(54) rekursiv gegebene Folge
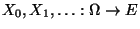 eine Markov-Kette ist, deren
Übergangsmatrix
eine Markov-Kette ist, deren
Übergangsmatrix
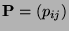 gegeben ist durch
falls
gegeben ist durch
falls
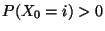 für jedes
für jedes 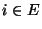 .
.
- Beispiel
 (Diffusionsmodell)
(Diffusionsmodell)
vgl. P. Brémaud (1999)
Markov Chains. Springer-Verlag, New York, S.76
- Beachte
-




Nächste Seite: Stationäre Anfangsverteilungen
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit; Perron-Frobenius-Theorem
Inhalt
Ursa Pantle
2003-09-29
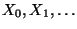 durch die Quasi-Positivität ihrer
Übergangsmatrix
durch die Quasi-Positivität ihrer
Übergangsmatrix
 charakterisiert.
charakterisiert.
 direkt nachzuweisen (insbesondere dann, wenn
direkt nachzuweisen (insbesondere dann, wenn 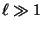 ).
).
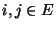 sagen
wir, dass der Zustand
sagen
wir, dass der Zustand 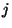 vom Zustand
vom Zustand 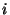 erreichbar ist,
falls
erreichbar ist,
falls
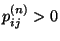 für ein
für ein 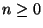 gilt, wobei
gilt, wobei
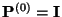 . (Schreibweise:
. (Schreibweise: 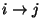 )
)
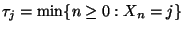 die Anzahl der Schritte
bis die Markov-Kette
die Anzahl der Schritte
bis die Markov-Kette 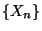 zum ersten Mal den Zustand
zum ersten Mal den Zustand 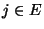 erreicht. Dabei setzen wir
erreicht. Dabei setzen wir
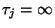 , falls
, falls 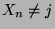 für
jedes
für
jedes  .
.
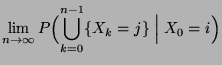
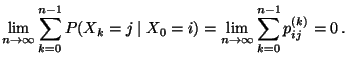
![$\displaystyle {\mathbf{P}}_1=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/2 & 1/2
\end{array}\right)$](img425.png) und
und![$\displaystyle \qquad
{\mathbf{P}}_2=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/4 & 3/4
\end{array}\right)
$](img426.png)