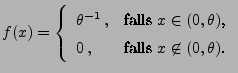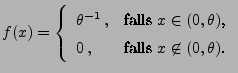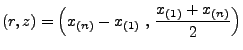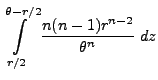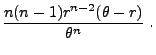Nächste Seite: Empirische Verteilungsfunktion
Aufwärts: Ordnungsstatistiken
Vorherige Seite: Absolutstetige Stichprobenvariablen
Inhalt
Beispiel: gleichverteilte Stichprobenvariablen
- Wir illustrieren nun die in Abschnitt 1.4.2
hergeleiteten Ergebnisse für das folgende Beispiel.
- Die Stichprobenvariablen
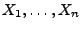 seien gleichverteilt im
Intervall
seien gleichverteilt im
Intervall
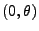 für ein
für ein 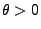 , d.h.
, d.h.
- Dichte, Erwartungswert und Varianz von
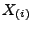
- Aus Theorem 1.15 ergibt sich durch Einsetzen in
(53), dass
- Hieraus folgt insbesondere, dass
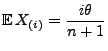
und
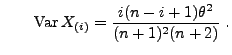
- Gemeinsame Dichte von
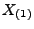 und
und 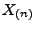
- Aus Theorem 1.16 ergibt sich durch Einsetzen in
(55), dass für
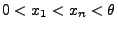
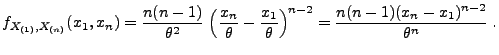 |
(57) |
- Gemeinsame Dichte von
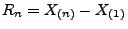 und
und
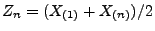
- Wir betrachten nun die Stichprobenspannweite
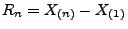 und das arithmetische Mittel
und das arithmetische Mittel
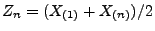 der
extremalen Ordnungsstatistiken
der
extremalen Ordnungsstatistiken 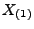 und
und 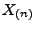 .
.
- Ähnlich wie das Stichprobenmittel
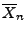 bzw. der
Stichprobenmedian
bzw. der
Stichprobenmedian 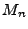 ist auch das Mittel
ist auch das Mittel
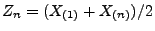 eine sogenannte
Lokationskenngröße.
eine sogenannte
Lokationskenngröße.
- Für die gemeinsame Dichte
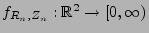 des
Zufallsvektors
des
Zufallsvektors 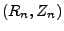 gilt
gilt
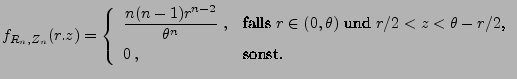 |
(58) |
- Dabei ergibt sich (58) aus (57)
und aus dem in Theorem 1.9 angegebenen
Transformationssatz für die Dichte von absolutstetigen
Zufallsvektoren.
- Denn durch die Abbildung
mit
wird die Menge
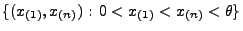 auf die Menge
auf die Menge
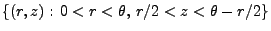 abgebildet, und
abgebildet, und
- für die Umkehrabbildung
mit
ist die Jacobi-Determinante gleich
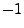 .
.
- Dichte von
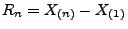
- Für die (Rand-) Dichte
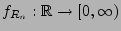 von
von
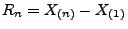 gilt
gilt
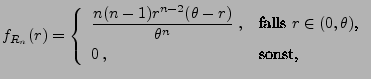 |
(59) |
- denn aus (58) und aus Theorem WR-3.9 über die
Integraldarstellung von Randdichten ergibt sich, dass für jedes
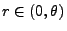
- Dichte von
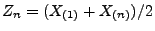
- Auf die gleiche Weise wie bei der Herleitung von
(59) kann man zeigen, dass
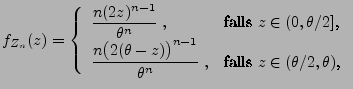 |
(60) |
- denn aus (58) ergibt sich, dass für
![$ z\in(0,\theta/2]$](img469.png) bzw. für
bzw. für
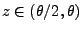




Nächste Seite: Empirische Verteilungsfunktion
Aufwärts: Ordnungsstatistiken
Vorherige Seite: Absolutstetige Stichprobenvariablen
Inhalt
Ursa Pantle
2004-07-14