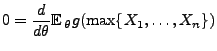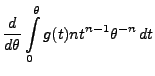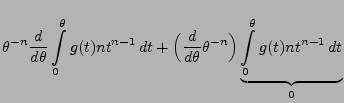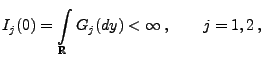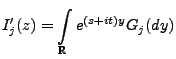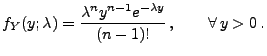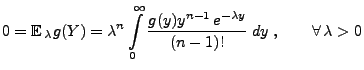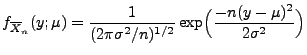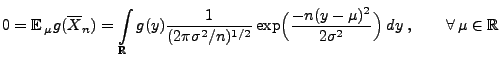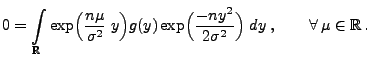Lemma 2.4
Für jede messbare Funktion
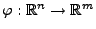
und für jede
messbare Abbildung
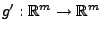
ist der Schätzer
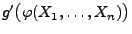
für
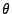
vollständig, falls
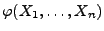
diese Eigenschaft
besitzt.
Lemma 2.5
Seien
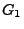
und
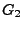
zwei
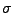
-endliche Maße über
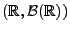
, die entweder beide diskret oder beide
absolutstetig sind. Falls die Integrale
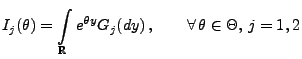 |
(47) |
existieren (und endlich sind) und falls
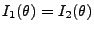
für jedes
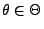
, dann gilt
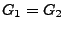
.
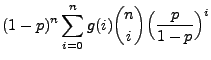
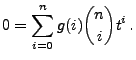
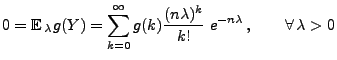
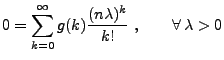
![$\displaystyle f_{\max \{X_1,\ldots,X_n\}}(t;\theta)=\left\{\begin{array}{ll}
n...
...x{falls
$t\in(0,\theta)$,}\\ [3\jot]
0 & \mbox{sonst.}
\end{array}\right.
$](img1186.png)