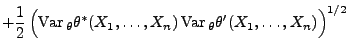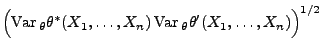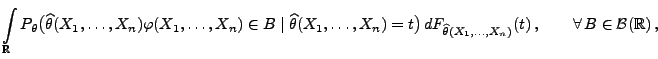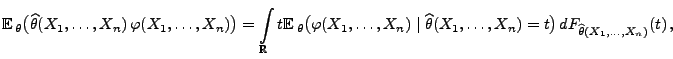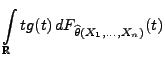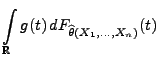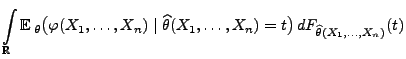- Sei
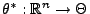 eine Stichprobenfunktion, so dass
für jedes
eine Stichprobenfunktion, so dass
für jedes
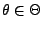
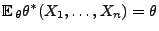 und
und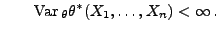
- Falls für jede Stichprobenfunktion
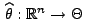 mit
die Ungleichung
mit
die Ungleichung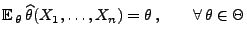 gilt, dann heißt
gilt, dann heißt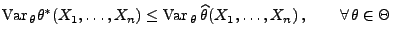
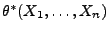 bester
erwartungstreuer Schätzer für
bester
erwartungstreuer Schätzer für 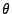 .
.
- Bevor wir zeigen, welche erwartungstreuen Schätzer beste erwartungstreue Schätzer sind, diskutieren wir zunächst einige grundlegende Eigenschaften solcher Schätzer.
- Als erstes zeigen wir den folgenden Eindeutigkeitssatz für beste erwartungstreue Schätzer.