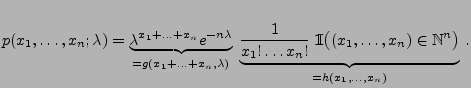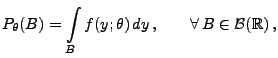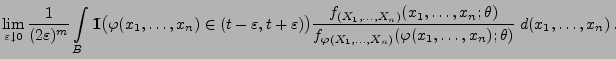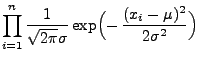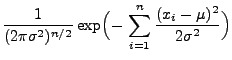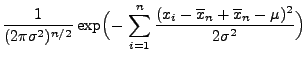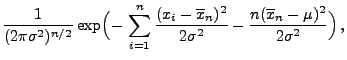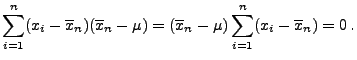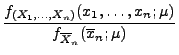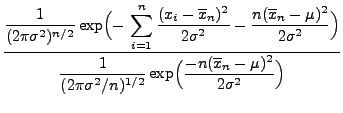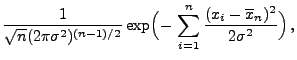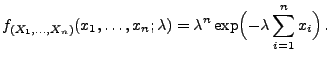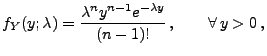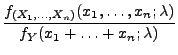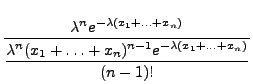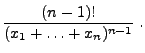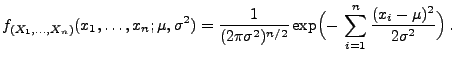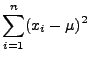Nächste Seite: Vollständigkeit
Aufwärts: Güteeigenschaften von Punktschätzern
Vorherige Seite: Ungleichung von Cramér-Rao
Inhalt
Suffizienz
Sei
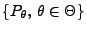 ein beliebiges parametrisches
Modell mit
ein beliebiges parametrisches
Modell mit
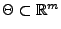 , und sei
, und sei
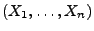 eine
Zufallsstichprobe über dem (kanonischen) Wahrscheinlichkeitsraum
eine
Zufallsstichprobe über dem (kanonischen) Wahrscheinlichkeitsraum
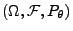 .
.
- Zur Erinnerung: Unter gewissen Regularitätsbedingungen hatten wir
in Abschnitt 2.3.2 für eine Klasse von
erwartungstreuen Schätzern eine untere Schranke für ihre Varianz,
die sogenannte Ungleichung von Cramér-Rao, hergeleitet; vgl.
Korollar 2.1.
- In Abschnitt 2.3.5 werden wir die Frage untersuchen,
unter welchen Bedingungen erwartungstreue Schätzer mit minimaler
Varianz existieren und welche Eigenschaften solche Schätzer haben.
- In Zusammenhang hiermit wird die Suffizienz von Schätzern eine
wichtige Rolle spielen, wobei diese Eigenschaft intuitiv wie folgt
beschrieben werden kann.
- Man sagt, dass der Schätzer
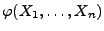 für
für 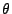 suffizient ist, falls (in einem noch zu präzisierenden Sinne)
sämtliche Information über
suffizient ist, falls (in einem noch zu präzisierenden Sinne)
sämtliche Information über 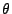 , die in der Zufallsstichprobe
, die in der Zufallsstichprobe
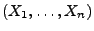 enthalten ist, auch in
enthalten ist, auch in
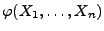 enthalten ist.
enthalten ist.
- Beachte
-
- Typischerweise erfolgt ein ,,Informationsverlust'' beim Übergang
von
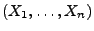 nach
nach
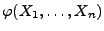 insofern,
dass
insofern,
dass
- die Funktionswerte der Abbildung
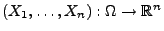 im allgemeinen nicht aus den Funktionswerten der Abbildung
im allgemeinen nicht aus den Funktionswerten der Abbildung
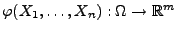 rekonstruiert werden
können.
rekonstruiert werden
können.
- Von Suffizienz spricht man, wenn dieser ,,Informationsverlust'' in
einem gewissen (stochastischen) Sinne nicht wesentlich ist.
Wir präzisieren dies zunächst für den diskreten Fall: Für
jedes
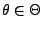 gelte
gelte
-
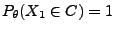 für eine abzählbare Menge
für eine abzählbare Menge
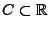 ,
die nicht von
,
die nicht von 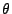 abhängt, wobei wir mit
abhängt, wobei wir mit
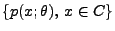 die Wahrscheinlichkeitsfunktion von
die Wahrscheinlichkeitsfunktion von 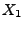 bezeichnen und
o.B.d.A. annehmen, dass
bezeichnen und
o.B.d.A. annehmen, dass
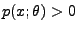 für jedes
für jedes 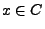 .
.
- Dann gilt auch
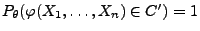 für jedes
für jedes
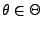 , wobei
, wobei
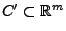 die
minimale abzählbare Menge mit dieser Eigenschaft sei, d.h., dass
die
minimale abzählbare Menge mit dieser Eigenschaft sei, d.h., dass
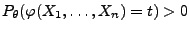 für jedes
für jedes
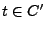 .
.
- Definition
 Der Schätzer
Der Schätzer
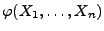 für
für 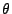 heißt suffizient, falls für beliebige
heißt suffizient, falls für beliebige
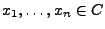 und
und
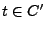 die bedingten Wahrscheinlichkeiten
die bedingten Wahrscheinlichkeiten
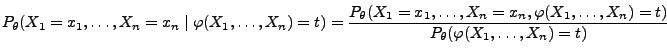 |
(42) |
nicht von 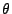 abhängen.
abhängen.
- Beachte
-
Zunächst zeigen wir, dass die Suffizienz bei (bijektiven)
zusammengesetzten Stichprobenfunktionen nicht verloren geht.
Lemma 2.1
Sei
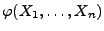
ein suffizienter Schätzer für
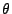
, und sei
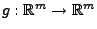
eine bijektive Borel-messbare
Abbildung. Dann ist auch
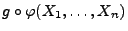
ein
suffizienter Schätzer für
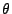
.
- Beweis
-
Für jedes
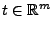 mit
mit
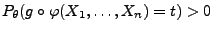 gilt
gilt
wobei der letzte Ausdruck nicht von 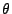 abhängt, weil
abhängt, weil
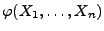 suffizient ist.
suffizient ist.

- Beachte
-
- Wir leiten nun eine (notwendige und hinreichende) Bedingung für
die Suffizienz von Schätzern her, die sich unmittelbar aus der
Definition dieser Güteeigenschaft ergibt.
- Dabei verwenden wir die abkürzende Schreibweise
für die Wahrscheinlichkeitsfunktion der Zufallsstichprobe
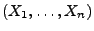 , und
für die Wahrscheinlichkeitsfunktion von
, und
für die Wahrscheinlichkeitsfunktion von
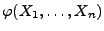 .
.
Lemma 2.2
Der Schätzer
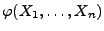
für
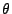
ist genau dann
suffizient, wenn für beliebige
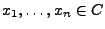
der Quotient
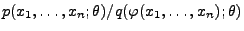
nicht von
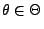
abhängt.
- Beweis
-
- Beispiel
 Bernoulli-verteilte Stichprobenvariablen
Bernoulli-verteilte Stichprobenvariablen
- Beachte
-
- Die folgende (verallgemeinerte) Fassung von
Lemma 2.2 wird in der Literatur
Faktorisierungssatz von Neyman-Fisher genannt.
- Dieser Faktorisierungssatz beinhaltet eine andere (notwendige und
hinreichende) Bedingung für die Suffizienz, die gegenüber der in
Lemma 2.2 angegebenen Bedingung den Vorteil besitzt,
dass die Wahrscheinlichkeitsfunktion von
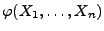 nicht explizit berechnet werden muss.
nicht explizit berechnet werden muss.
Theorem 2.3
Der Schätzer
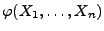
für
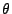
ist genau dann
suffizient, wenn es Borel-messbare Funktionen
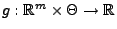
und
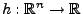
gibt, so dass
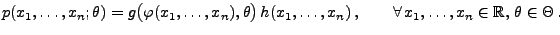 |
(43) |
- Beweis
-
- Beispiel
 Poissonverteilte Stichprobenvariablen
Poissonverteilte Stichprobenvariablen
Wir betrachten nun den absolutstetigen Fall, d.h.,
- Definition
 Der Schätzer
Der Schätzer
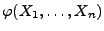 für
für 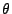 heißt
suffizient, falls für beliebige
heißt
suffizient, falls für beliebige
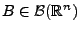 und
und
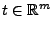 die bedingte Wahrscheinlichkeit
die bedingte Wahrscheinlichkeit
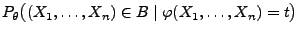 nicht von
nicht von 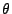 abhängt.
abhängt.
- Beachte
-
- Ähnlich wie im diskreten Fall (vgl. Lemma 2.2) kann
man auch im absolutstetigen Fall zunächst eine (hinreichende)
Bedingung für die Suffizienz von Schätzern angeben, die direkt an
die Definition dieser Güteeigenschaft anknüpft.
- Um die Gültigkeit dieser Bedingung überprüfen zu können, ist dabei
jedoch die Kenntnis der Dichte des Schätzers
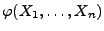 erforderlich.
erforderlich.
Lemma 2.3
Sei
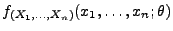
die Dichte der
Zufallsstichprobe
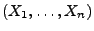
, und
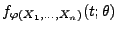
sei die Dichte von
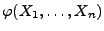
. Falls für beliebige
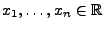
mit
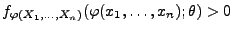 |
(46) |
der Quotient
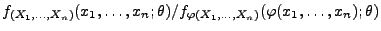
nicht von
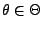
abhängt, dann ist durch
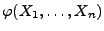
ein suffizienter
Schätzer für
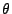
gegeben.
- Beweis
-
- Beispiele
-
 Normalverteilte Stichprobenvariablen
Normalverteilte Stichprobenvariablen
 Exponentialverteilte Stichprobenvariablen
Exponentialverteilte Stichprobenvariablen
- Beachte
-
- Es ist jedoch oft schwierig, die Dichte des Schätzers
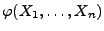 zu bestimmen und die Gültigkeit der in
Lemma 2.3 angegebenen Bedingung nachzuprüfen.
zu bestimmen und die Gültigkeit der in
Lemma 2.3 angegebenen Bedingung nachzuprüfen.
- So wie im diskreten Fall liefert dann die folgende Variante des
Faktorisierungssatzes von Neyman-Fisher eine alternative
(leichter nachprüfbare) Bedingung für die Suffizienz.
Theorem 2.4
Der Schätzer
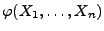
für
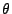
ist genau dann
suffizient, wenn es Borel-messbare Funktionen
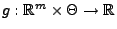
und
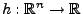
gibt, so dass
Der Beweis von Theorem 2.4 geht über den
Rahmen dieser einführenden Vorlesung hinaus; vgl. beispielsweise
Abschnitt 3.3 in H. Pruscha (2000) Vorlesungen über
Mathematische Statistik, Teubner-Verlag, Stuttgart, oder
Abschnitt 2.6 in E.L. Lehmann (1997) Testing Statistical
Hypotheses, 2nd ed., Springer-Verlag, New York.
- Beispiel
 Normalverteilte Stichprobenvariablen
(Fortsetzung)
Normalverteilte Stichprobenvariablen
(Fortsetzung)




Nächste Seite: Vollständigkeit
Aufwärts: Güteeigenschaften von Punktschätzern
Vorherige Seite: Ungleichung von Cramér-Rao
Inhalt
Ursa Pantle
2004-07-14
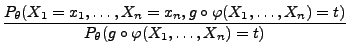
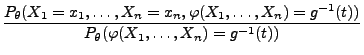
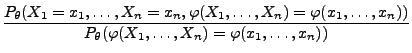
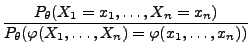
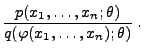
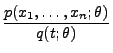
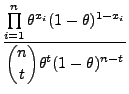
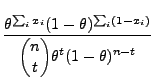
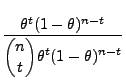
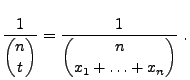
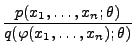
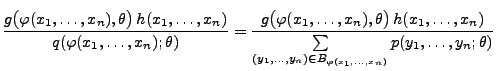
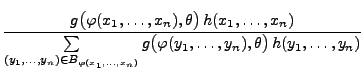
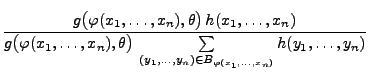
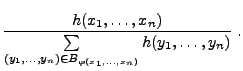
![$\displaystyle p(x_1,\ldots,x_n;\lambda)=\left\{\begin{array}{ll}
\frac{\lambda...
...dots,x_n\in\mathbb{N}$,}\\ [3\jot]
0\,, & \mbox{sonst.}
\end{array}\right.
$](img1098.png)