



Nächste Seite: Maßtheoretische Definition der bedingten
Aufwärts: Güteeigenschaften von Punktschätzern
Vorherige Seite: Beste erwartungstreue Schätzer
Inhalt
Bedingte Erwartung; Ungleichung von Rao-Blackwell
- Definition
- Die zufällige Stichprobenfunktion
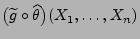 wird in der Literatur
die bedingte Erwartung von
wird in der Literatur
die bedingte Erwartung von
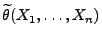 bezüglich
bezüglich
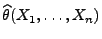 genannt und mit
genannt und mit
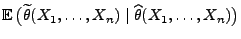 bezeichnet.
bezeichnet.
Auf ähnliche Weise wie Theorem 2.5 lässt sich dann
die folgende Aussage aus Lemma 2.7 herleiten.
Theorem 2.6
- Sei
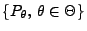 ein beliebiges
parametrisches Modell mit
ein beliebiges
parametrisches Modell mit
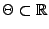 , und seien
, und seien
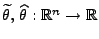 beliebige
Stichprobenfunktionen, so dass
beliebige
Stichprobenfunktionen, so dass
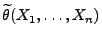 ein erwartungstreuer Schätzer und
ein erwartungstreuer Schätzer und
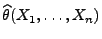 ein vollständiger und suffizienter Schätzer für
ein vollständiger und suffizienter Schätzer für 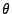 ist,
wobei
ist,
wobei
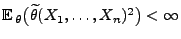 für jedes
für jedes
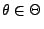 .
.
- Dann ist die bedingte Erwartung
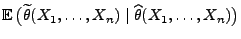 bester erwartungstreuer
Schätzer für
bester erwartungstreuer
Schätzer für 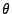 .
.
- Beweis
-
- Beweis
 Die Behauptung ergibt sich unmittelbar aus
Theorem 2.6, denn kann man zeigen, dass
vgl. Teilaussage 4 in Theorem 2.8.
Die Behauptung ergibt sich unmittelbar aus
Theorem 2.6, denn kann man zeigen, dass
vgl. Teilaussage 4 in Theorem 2.8.

Wir betrachten nun noch eine abgeschwächte Version von
Theorem 2.6, die besagt, dass durch den Übergang zur
bedingten Erwartung
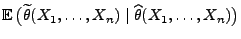 auch dann eine
Verbesserung der Schätzgenauigkeit erzielt werden kann, wenn
nicht vorausgesetzt wird, dass
auch dann eine
Verbesserung der Schätzgenauigkeit erzielt werden kann, wenn
nicht vorausgesetzt wird, dass
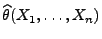 vollständig ist.
vollständig ist.
- Beweis
-
- Im Beweis von Theorem 2.6 hatten wir gezeigt, dass
und
- Hieraus ergibt sich die Behauptung, weil
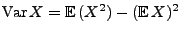 für jede Zufallsvariable
für jede Zufallsvariable 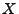 mit
mit
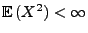 .
.

- Beachte
-
- Die Ungleichung (54) wird in der Literatur
Ungleichung von Rao-Blackwell genannt.
- Weil in Theorem 2.7 nicht vorausgesetzt wird, dass
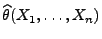 vollständig ist, muss die
bedingte Erwartung
vollständig ist, muss die
bedingte Erwartung
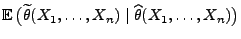 nicht notwendig bester
erwartungstreuer Schätzer für
nicht notwendig bester
erwartungstreuer Schätzer für 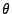 sein.
sein.




Nächste Seite: Maßtheoretische Definition der bedingten
Aufwärts: Güteeigenschaften von Punktschätzern
Vorherige Seite: Beste erwartungstreue Schätzer
Inhalt
Ursa Pantle
2004-07-14
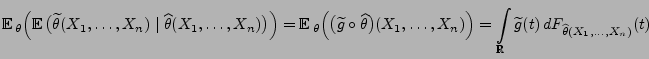
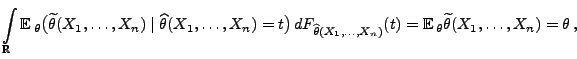
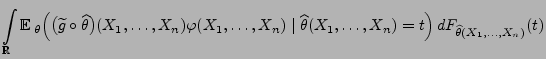
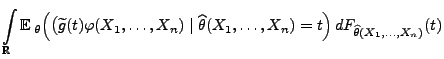
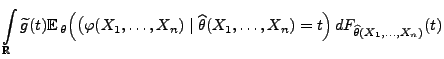
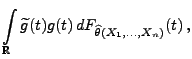
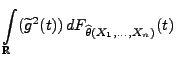
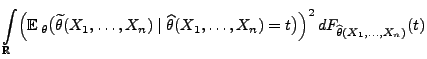
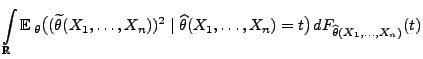
![]() auch dann eine
Verbesserung der Schätzgenauigkeit erzielt werden kann, wenn
nicht vorausgesetzt wird, dass
auch dann eine
Verbesserung der Schätzgenauigkeit erzielt werden kann, wenn
nicht vorausgesetzt wird, dass
![]() vollständig ist.
vollständig ist.