- Wir nehmen an, dass
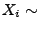 N
N
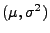 für ein
(unbekanntes)
für ein
(unbekanntes)
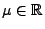 und ein (bekanntes)
und ein (bekanntes)
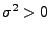 .
.
- Für einen vorgegebenen (hypothetischen) Zahlenwert
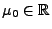 soll die Hypothese
soll die Hypothese
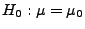 (gegen die Alternative
(gegen die Alternative
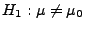 ) getestet werden, d.h.
) getestet werden, d.h.
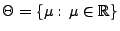 mit
mit
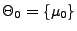 bzw.
bzw.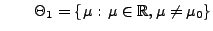
- Wir betrachten die Testgröße
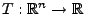 mit
mit
- und den Schwellenwert
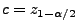 , d.h. das
, d.h. das
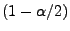 -Quantil der Standardnormalverteilung.
-Quantil der Standardnormalverteilung.
- Weil
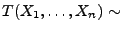 N
N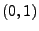 , gilt dann
, gilt dann
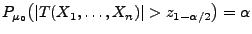 .
.
- Die Hypothese
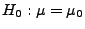 wird abgelehnt, falls
wird abgelehnt, falls
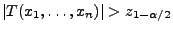 .
.
Für
![]() und
und
![]() wollen wir nun prüfen, ob
wollen wir nun prüfen, ob
- die Hypothese
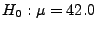 mit der bereits in
Abschnitt 3.2.1 betrachteten (konkreten) Stichprobe
vereinbar ist.
mit der bereits in
Abschnitt 3.2.1 betrachteten (konkreten) Stichprobe
vereinbar ist.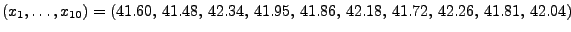
- In diesem Fall gilt
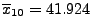 , und aus
(7) ergibt sich somit
, und aus
(7) ergibt sich somit
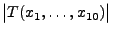
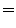
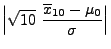
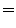
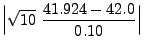
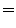
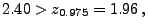
wobei das Quantil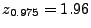 aus Tabelle 1 entnommen wurde.
aus Tabelle 1 entnommen wurde.
- Die Hypothese
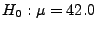 wird also verworfen.
wird also verworfen.
- Wir betrachten die Gütefunktion
![$ \alpha_n:\mathbb{R}\to[0,1]$](img2015.png) dieses
Tests.
dieses
Tests.
- Für beliebige
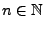 und
und
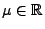 gilt
gilt
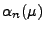
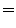
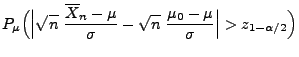
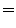
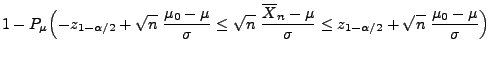
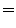
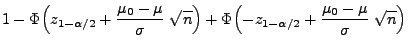
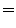
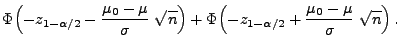
- Hieraus ergibt sich, dass die Ableitung
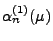 für
jedes
für
jedes 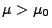 positiv ist und dass
positiv ist und dass
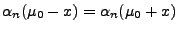 für jedes
für jedes
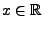 .
.
- Somit gilt
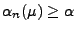 für beliebige
für beliebige
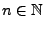 und
und
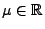 , und
, und
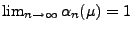 für jedes
für jedes
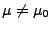 .
.
- Der Test ist also unverfälscht und konsistent.
- Für beliebige
- Falls die Hypothese
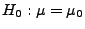 gegen die (einseitige)
Alternative
gegen die (einseitige)
Alternative
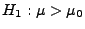 getestet werden soll, d.h.
getestet werden soll, d.h.
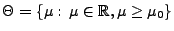 mit
dann könnte man zwar so wie bisher vorgehen und für die in (7) definierte Testgröße
mit
dann könnte man zwar so wie bisher vorgehen und für die in (7) definierte Testgröße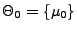 bzw.
bzw.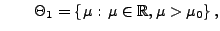
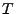
- den kritischen Bereich
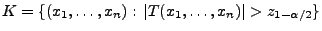 betrachten.
betrachten.
- Ein besserer Test ergibt sich jedoch, wenn der folgende
(einseitige) kritische Bereich
betrachtet wird, denn es gilt
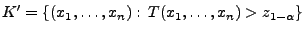
wobei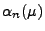 bzw.
bzw.
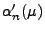 die Macht des
Tests mit dem kritischen Bereich
die Macht des
Tests mit dem kritischen Bereich 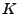 bzw.
bzw. 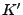 bezeichnet,
d.h.
bzw.
bezeichnet,
d.h.
bzw.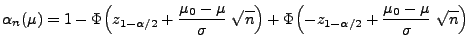
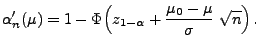
- Um die Gültigkeit der Ungleichung (8) einzusehen,
betrachten wir die Funktion
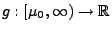 mit
mit
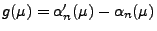 .
.
- Offenbar gilt
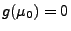 und
und
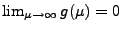 .
.
- Außerdem gilt
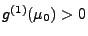 sowie
sowie
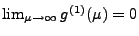 gilt, wobei
gilt, wobei 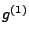 die
Ableitung von
die
Ableitung von 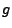 bezeichnet.
bezeichnet.
- Darüber hinaus kann man sich leicht davon überzeugen, dass
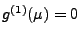 für genau ein
für genau ein 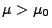 .
.
- Hieraus folgt, dass
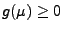 für jedes
für jedes
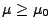 .
.
- Offenbar gilt
- den kritischen Bereich
- Falls die Hypothese
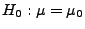 gegen die Alternative
gegen die Alternative
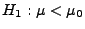 getestet werden soll, dann wird der kritische
Bereich
getestet werden soll, dann wird der kritische
Bereich
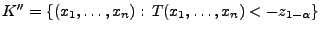 betrachtet.
betrachtet.