



Nächste Seite: Wiener-Prozess
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Eingebettete Markow-Ketten; Simulationsalgorithmus
Inhalt
Stationäre Anfangsverteilungen
Ähnlich wie bei Markow-Ketten mit diskreter Zeit (vgl. Abschnitt
MK-2.2.4) betrachten wir nun eine spezielle Klasse von
Anfangsverteilungen, die invariant bezüglich der Übergangsfunktion
von Markow-Prozessen sind.
- Definition
 Die Wahrscheinlichkeitsfunktion
Die Wahrscheinlichkeitsfunktion
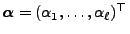 heißt stationäre Anfangsverteilung bezüglich der Übergangsfunktion
heißt stationäre Anfangsverteilung bezüglich der Übergangsfunktion
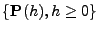 , falls
, falls
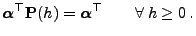 |
(46) |
- Beachte

- Definition
 Die Übergangsfunktion
Die Übergangsfunktion
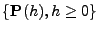 heißt irreduzibel, falls
heißt irreduzibel, falls
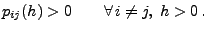 |
(47) |
- Beachte
 Man kann leicht zeigen, dass
Man kann leicht zeigen, dass
- die Bedingung (47) mit der Irreduzibilität der
Intensitätsmatrix
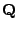 äquivalent ist,
äquivalent ist,
- d.h., für beliebige
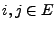 mit
mit 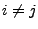 gibt es eine Folge
von Zuständen
gibt es eine Folge
von Zuständen
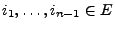 mit
mit
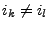 , so dass
, so dass
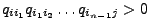 .
.
Das folgende Theorem zeigt darüber hinaus: Die Irreduzibilität der
Übergangsfunktion
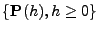 bzw. der
Intensitätsmatrix
bzw. der
Intensitätsmatrix
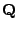 impliziert, dass es eine (eindeutig
bestimmte) stationäre Anfangsverteilung bezüglich der
Übergangsfunktion
impliziert, dass es eine (eindeutig
bestimmte) stationäre Anfangsverteilung bezüglich der
Übergangsfunktion
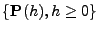 gibt.
gibt.
Theorem 2.20
Wenn die Übergangsfunktion
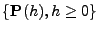
irreduzibel ist,
dann existiert der Grenzwert
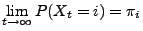 |
(48) |
für jedes
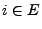
, wobei
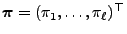
die (eindeutig bestimmte) stationäre Anfangsverteilung bezüglich
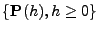
ist.
- Beweis

- Beachte





Nächste Seite: Wiener-Prozess
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Eingebettete Markow-Ketten; Simulationsalgorithmus
Inhalt
Ursa Pantle
2005-07-13
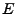 gilt für jede
stationäre Anfangsverteilung
gilt für jede
stationäre Anfangsverteilung
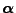 :
:
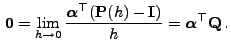
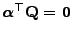 folgt die Gültigkeit von
folgt die Gültigkeit von
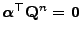 und somit auch
und somit auch
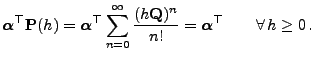
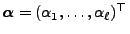 , die der Gleichung
(46) genügt, bzw. die eindeutige Lösbarkeit von
(46) nicht immer gewährleistet sein.
, die der Gleichung
(46) genügt, bzw. die eindeutige Lösbarkeit von
(46) nicht immer gewährleistet sein.
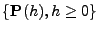 folgt, dass
folgt, dass
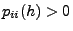 für beliebige
für beliebige 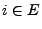 und
und 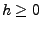 .
.