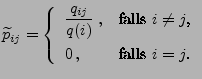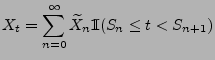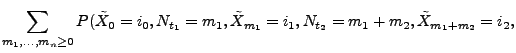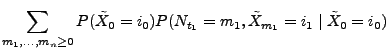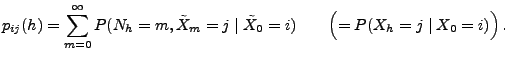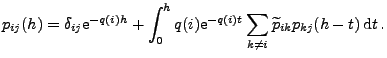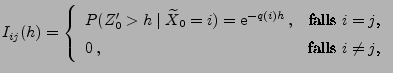Nächste Seite: Stationäre Anfangsverteilungen
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Kolmogorowsche Differentialgleichungen
Inhalt
Eingebettete Markow-Ketten; Simulationsalgorithmus
- Schritt 1
 Sei
Sei 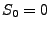 und
und
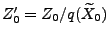 , wobei
, wobei
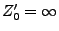 gesetzt wird, falls
gesetzt wird, falls
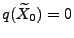 .
.
- Die Zufallsvariable
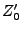 ist die Aufenthaltsdauer
des zu konstruierenden Markow-Prozesses
ist die Aufenthaltsdauer
des zu konstruierenden Markow-Prozesses  im (zufälligen)
Anfangszustand
im (zufälligen)
Anfangszustand
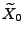 , der zum Zeitpunkt
, der zum Zeitpunkt 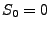 gewählt
wird.
gewählt
wird.
- Dabei gilt
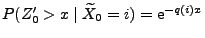 für jedes
für jedes 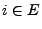 mit
mit
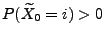 ;
; 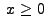 .
.
- Schritt 2
 Sei
Sei
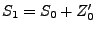 und
und
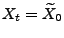 für
für
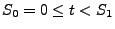 , wodurch die Trajektorie von
, wodurch die Trajektorie von  bis zum
ersten Sprungzeitpunkt
bis zum
ersten Sprungzeitpunkt 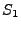 gegeben ist.
gegeben ist.
- Schritt 3
 (analog zu Schritt 1) Sei
(analog zu Schritt 1) Sei
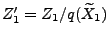 , wodurch
, wodurch
- die Aufenthaltsdauer von
 im Zustand
im Zustand
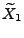 gegeben ist, der zum Zeitpunkt
gegeben ist, der zum Zeitpunkt 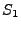 gewählt wird.
gewählt wird.
- Dabei gilt
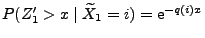 , falls
, falls
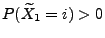 .
.
- Schritt 4
 Sei
Sei
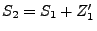 und
und
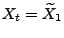 für
für
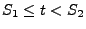 .
.

- Schritt
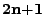
 Wir nehmen nun an, dass
die Größen
Wir nehmen nun an, dass
die Größen
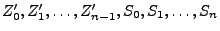 und
und
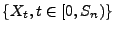 für ein
für ein 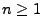 bereits definiert
worden sind, und setzen
bereits definiert
worden sind, und setzen
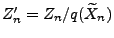 .
.
- Schritt
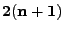
 Sei
Sei
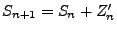 und
und
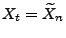 für
für
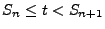 .
.
- Beachte

- Auf diese Weise lassen sich die Trajektorien von
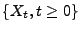 für beliebige
für beliebige  konstruieren, weil man sich leicht
überlegen kann, dass
konstruieren, weil man sich leicht
überlegen kann, dass
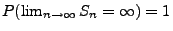 .
.
- Somit ist durch das oben beschriebene Konstruktionsprinzip ein
Algorithmus zur Simulation des zeitstetigen Prozesses
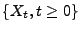 gegeben, wobei vorausgesetzt wird, dass
Algorithmen
gegeben, wobei vorausgesetzt wird, dass
Algorithmen
- zur Simulation der Folge
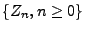 von unabhängigen und
Exp
von unabhängigen und
Exp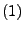 -verteilten Zufallsvariablen sowie
-verteilten Zufallsvariablen sowie
- der eingebetteten Marlow-Kette
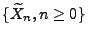 (vgl.
Übungsaufgabe 3.7)
(vgl.
Übungsaufgabe 3.7)
vorhanden sind.
- Außerdem kann man zeigen, dass die endlich-dimensionalen
Verteilungen des Prozesses
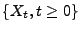 die
Faktorisierungeigenschaft besitzen, die in der
Definitionsgleichung (10) von Markow-Prozessen
postuliert wird.
die
Faktorisierungeigenschaft besitzen, die in der
Definitionsgleichung (10) von Markow-Prozessen
postuliert wird.
Theorem 2.18
Der in
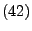
gegebene stochastische Prozess
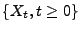
ist ein homogener
Markow-Prozess.
- Beweis

Wir zeigen nun, dass der in diesem Abschnitt konstruierte
stochastische Prozess
 der ,,richtige''
Markow-Prozess ist, d.h., seine Intensitätsmatrix ist gleich der
vorgegebenen Matrix
der ,,richtige''
Markow-Prozess ist, d.h., seine Intensitätsmatrix ist gleich der
vorgegebenen Matrix
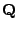 .
.
- Hierfür muss gezeigt werden, dass sich die
Übergangswahrscheinlichkeiten
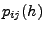 des Markow-Prozesses
des Markow-Prozesses
 durch die ,,lokalen''
Charakteristiken
durch die ,,lokalen''
Charakteristiken
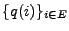 und
und
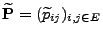 ausdrücken
lassen.
ausdrücken
lassen.
- Dabei sagt man, dass
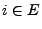 ein absorbierender Zustand
ist, falls
ein absorbierender Zustand
ist, falls 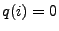 .
.
Theorem 2.19
Für beliebige
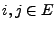
und
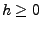
gilt
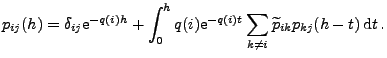 |
(44) |
Insbesondere gilt
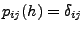
für beliebige
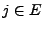
und
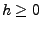
, wenn
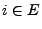
ein absorbierender Zustand ist.
- Beweis

- Beweis
 Um (45) zu beweisen, genügt es,
in (44) die Ableitung bezüglich
Um (45) zu beweisen, genügt es,
in (44) die Ableitung bezüglich 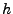 zu bilden und
danach den Grenzwert für
zu bilden und
danach den Grenzwert für
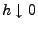 zu betrachten.
zu betrachten.

- Beachte
 Wenn man die Formeln (13) und
(45) miteinander vergleicht, dann erkennt man, dass
die Intensitätsmatrix des in diesem Abschnitt konstruierten
Markow-Prozesses
Wenn man die Formeln (13) und
(45) miteinander vergleicht, dann erkennt man, dass
die Intensitätsmatrix des in diesem Abschnitt konstruierten
Markow-Prozesses
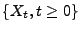 mit der vorgegebenen Matrix
mit der vorgegebenen Matrix
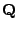 übereinstimmt.
übereinstimmt.
- Beispiel

- Der in diesem Abschnitt konstruierte Markow-Prozess
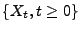 heißt Geburts- und Todesprozess, wenn
heißt Geburts- und Todesprozess, wenn
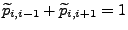 für beliebige
für beliebige 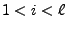 und
und
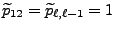 gilt.
gilt.
- Die Produkte
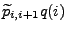 und
und
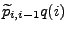 heißen Geburtsrate bzw. Sterberate.
heißen Geburtsrate bzw. Sterberate.
- Diese Begriffsbildungen lassen sich damit begründen, dass die
Größen
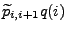 und
und
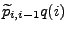 gemäß Korollar 2.3 mit den Übergangsintensitäten
gemäß Korollar 2.3 mit den Übergangsintensitäten
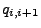 und
und 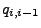 für die Übergänge
für die Übergänge 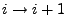 bzw.
bzw.
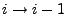 im Sinne der Definitionsgleichung (13)
übereinstimmen.
im Sinne der Definitionsgleichung (13)
übereinstimmen.




Nächste Seite: Stationäre Anfangsverteilungen
Aufwärts: Markow-Prozesse mit endlich vielen
Vorherige Seite: Kolmogorowsche Differentialgleichungen
Inhalt
Ursa Pantle
2005-07-13
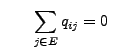
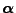 eine beliebige Anfangsverteilung, und sei
eine beliebige Anfangsverteilung, und sei
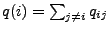 für jedes
für jedes 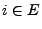 .
.
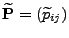 gegeben durch
gegeben durch
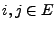 mit
mit 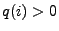 .
.
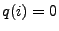 , dann wird die
, dann wird die 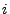 -te Zeile von
-te Zeile von
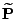 gleich
gleich
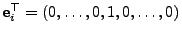 gesetzt, wobei die
gesetzt, wobei die
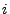 -te Komponente von
-te Komponente von
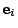 gleich
gleich  ist.
ist.
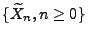 eine Markow-Kette mit der
Anfangsverteilung
eine Markow-Kette mit der
Anfangsverteilung
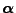 und der Übergangsmatrix
und der Übergangsmatrix
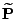 .
.