



Nächste Seite: Darstellung als Markow-Prozess bzw.
Aufwärts: Wiener-Prozess
Vorherige Seite: Eigenschaften normalverteilter Zufallsvariablen
Inhalt
Konstruktion von Wiener-Prozessen; Simulationsalgorithmus
Aus Lemma 2.7 ergibt sich, dass man
- Beachte

Insgesamt ergibt sich nun der folgende Ansatz zur Konstruktion von
Wiener-Prozessen in ![$ [0,1]$](img566.png) .
.
- Beweis
-
- Mit Hilfe von (7) ergibt sich aus der ersten
Teilaussage von Lemma 2.8, dass die in
(13) eingeführte Größe
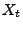 für jedes
für jedes ![$ t\in[0,1]$](img79.png) eine wohldefinierte (normalverteilte) Zufallsvariable ist, wobei
eine wohldefinierte (normalverteilte) Zufallsvariable ist, wobei
![$\displaystyle X_t\sim{\rm N}(0,t)\qquad\forall\,t\in[0,1]\,.$](img1053.png) |
(14) |
- Denn es gilt
- Dabei ergibt sich die vorletzte Gleichheit aus
Lemma 2.5, weil
![$ {1\hspace{-1mm}{\rm I}}([0,t])\in L_2$](img1055.png) und weil somit
aus (5) folgt, dass
und weil somit
aus (5) folgt, dass
- Außerdem gilt
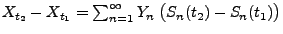 für beliebige
für beliebige
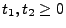 mit
mit
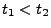 ,
,
- und ähnlich wie beim Beweis von (14) kann man
zeigen, dass
- weil
- d.h. insbesondere, dass die Zuwächse
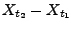 des
stochastischen Prozesses
des
stochastischen Prozesses  normalverteilt sind.
normalverteilt sind.
- Wir zeigen nun, dass
 ein Prozess mit unabhängigen
Zuwächsen ist.
ein Prozess mit unabhängigen
Zuwächsen ist.
- Aus (12) ergibt sich, dass für beliebige
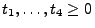 mit
mit
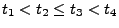
- Dabei ist
wobei sich die vorletzte Gleichheit erneut aus Formel
(5) in Lemma 2.5 ergibt.
- Somit gilt
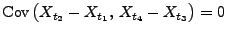 ,
und aus der zweiten Teilaussage von Lemma 2.8 ergibt
sich nun, dass
,
und aus der zweiten Teilaussage von Lemma 2.8 ergibt
sich nun, dass  unabhängige Zuwächse hat.
unabhängige Zuwächse hat.
- Schließlich ergibt sich aus der dritten Teilaussage von
Lemma 2.6 und aus Lemma 2.7, dass
sämtliche Trajektorien des Prozess
![$ \{X_t,\,t\in [0,1]\}$](img72.png) über dem
eingeschränkten Wahrscheinlichkeitsraum
über dem
eingeschränkten Wahrscheinlichkeitsraum
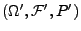 stetige Funktionen sind,
weil
stetige Funktionen sind,
weil
- die Summe
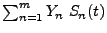 für jedes
für jedes 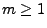 eine
stetige Funktion in
eine
stetige Funktion in 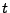 ist und
ist und
- die Konvergenz
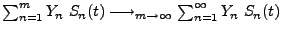 gleichmäßig in
gleichmäßig in 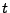 erfolgt.
erfolgt.
- Weil offenbar auch
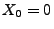 gilt, ist damit die Behauptung
vollständig bewiesen.
gilt, ist damit die Behauptung
vollständig bewiesen.

- Beachte

- Beachte
-
- Die in Abschnitt 2.4.3 enthaltenen Darlegungen lassen
sich auf völlig analoge Weise
- zur Konstruktion und Simulation von Wiener-Prozessen in
beliebigen beschränkten Intervallen der Form
![$ I=[0,c]$](img1102.png) verwenden,
wobei
verwenden,
wobei 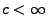 eine beliebige positive Zahl ist.
eine beliebige positive Zahl ist.
- Denn man kann sich leicht überlegen, dass
![$ \{Y_t,\,t\in[0,c]\}$](img1103.png) mit
mit
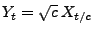 ein Wiener-Prozess in
ein Wiener-Prozess in ![$ [0,c]$](img1105.png) ist,
wenn
ist,
wenn
![$ \{X_t,\,t\in [0,1]\}$](img72.png) ein Wiener-Prozess in
ein Wiener-Prozess in ![$ [0,1]$](img566.png) ist;
vgl. auch Theorem 2.24 in
Abschnitt 2.4.6.
ist;
vgl. auch Theorem 2.24 in
Abschnitt 2.4.6.
- Wir erwähnen nun noch eine Möglichkeit, wie Wiener-Prozesse in
dem unbeschränkten Intervall
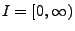 auf einfache Weise
konstruiert werden können.
auf einfache Weise
konstruiert werden können.




Nächste Seite: Darstellung als Markow-Prozess bzw.
Aufwärts: Wiener-Prozess
Vorherige Seite: Eigenschaften normalverteilter Zufallsvariablen
Inhalt
Ursa Pantle
2005-07-13
![]() .
.
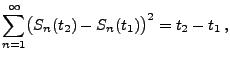
![$\displaystyle X_t=\left\{\begin{array}{ll} X_t^{(1)} & \mbox{für $t\in[0,1]$,}\...
...}+ X_{t-(n-1)}^{(n)}&
\mbox{für $t\in[n-1,n]$,}\\ \vdots &
\end{array}\right.
$](img1109.png)