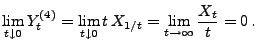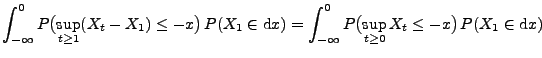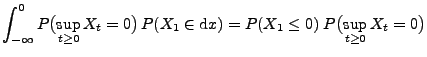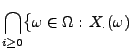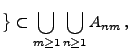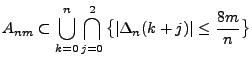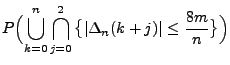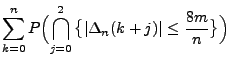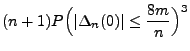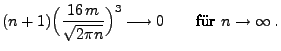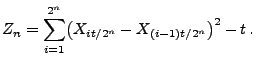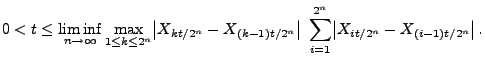Nächste Seite: Lévy-Prozesse und Martingale
Aufwärts: Wiener-Prozess
Vorherige Seite: Verteilung des Maximums
Inhalt
Weitere Verteilungs-
und Pfadeigenschaften
Wir zeigen nun einige Invarianzeigenschaften des
Wiener-Prozesses in
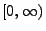 , womit die Tatsache gemeint ist,
dass bestimmte Transformationen des Wiener-Prozesses erneut zu
einem Wiener-Prozess führen.
, womit die Tatsache gemeint ist,
dass bestimmte Transformationen des Wiener-Prozesses erneut zu
einem Wiener-Prozess führen.
- Beweis
-
- Wir zeigen, dass die Prozesse
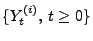 für
für
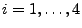 die vier Bedingungen in der Definition des
Wiener-Prozesses erfüllen.
die vier Bedingungen in der Definition des
Wiener-Prozesses erfüllen.
- Man kann sich leicht überlegen, dass die Prozesse
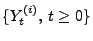 unabhängige Zuwächse besitzen mit
unabhängige Zuwächse besitzen mit
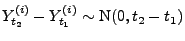 für
für
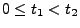 und
und
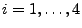 ,
,
- Offenbar gilt auch
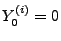 für
für
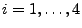 .
.
- Außerdem ist klar, dass die Prozesse
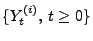 für
für
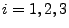 stetige Trajektorien besitzen.
stetige Trajektorien besitzen.
- Es bleibt also noch zu zeigen,
- Weil die Trajektorien von
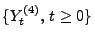 für jedes
für jedes 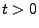 stetig sind, gilt
wobei
stetig sind, gilt
wobei
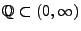 die (abzählbar unendliche) Menge der
positiven rationalen Zahlen ist.
die (abzählbar unendliche) Menge der
positiven rationalen Zahlen ist.
- Hieraus folgt, dass
- wobei
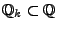 die (endliche) Menge der ,,ersten''
die (endliche) Menge der ,,ersten'' 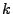 rationalen Zahlen ist
rationalen Zahlen ist
- und sich die letzte Gleichheit aus der Tatsache ergibt, dass die
(endlich-dimensionalen) Zufallsvektoren
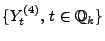 und
und
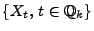 identisch verteilt sind.
identisch verteilt sind.
- Weil die Trajektorien des Wiener-Prozesses
![$ \{X_t^,\,t\in[0,1]\}$](img1244.png) rechtsseitig stetig in
rechtsseitig stetig in 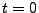 sind, ist der letzte Grenzwert gleich
sind, ist der letzte Grenzwert gleich
 . Damit ist (35) bewiesen.
. Damit ist (35) bewiesen.

- Beachte
 Die Gültigkeit von (35) kann
auch direkt aus Korollar 2.4 gefolgert werden, denn
es gilt
Die Gültigkeit von (35) kann
auch direkt aus Korollar 2.4 gefolgert werden, denn
es gilt
Korollar 2.5

Sei
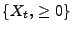
ein Wiener-Prozess. Dann gilt
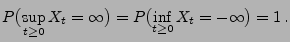 |
(36) |
- Beweis
-
- Beachte
-
- Die Aussage von Korollar 2.5 ist äquivalent mit
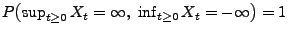 .
.
- Hieraus folgt insbesondere, dass fast alle Pfade des
Wiener-Prozesses
 in dem unbeschränkten
Intervall
in dem unbeschränkten
Intervall
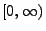 unendlich oft zwischen positiven und
negativen Werten oszillieren.
unendlich oft zwischen positiven und
negativen Werten oszillieren.
- Wir zeigen nun, dass die Pfade des Wiener-Prozesses

- auch in beschränkten Intervallen ,,wild'' oszillieren,
- denn es stellt sich heraus, dass sie zwar stetige, jedoch mit
Wahrscheinlichkeit
 nirgendwo differenzierbare Funktionen sind.
nirgendwo differenzierbare Funktionen sind.
Theorem 2.25

Sei
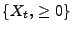
ein Wiener-Prozess. Dann gilt
- Beweis
-
- Wegen der Identität
genügt es zu zeigen, dass
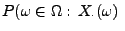 ist nirgendwo differenzierbar in
ist nirgendwo differenzierbar in
![$ [0,1]$](img566.png)
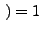 bzw., äquivalent hierzu, dass
bzw., äquivalent hierzu, dass
- Um die Gültigkeit von (39) zu beweisen, setzen wir
für beliebige natürliche Zahlen
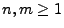
- Dann gilt
- und es genügt somit zu zeigen, dass
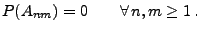 |
(40) |
- Sei
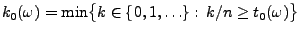 . Dann gilt für jedes
. Dann gilt für jedes
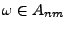 und
für
und
für 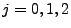
- Mit der Schreibweise
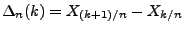 gilt also
und somit
gilt also
und somit
- Weil
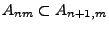 für jedes
für jedes 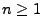 , ergibt sich
hieraus die Gültigkeit von (40).
, ergibt sich
hieraus die Gültigkeit von (40).

Korollar 2.6

Mit Wahrscheinlichkeit

gilt
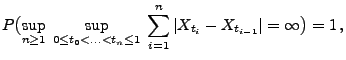 |
(41) |
d.h., fast alle Trajektorien des Wiener-Prozesses
![$ \{X_t,\,t\in [0,1]\}$](img72.png)
sind Funktionen mit unbeschränkter
Variation.
- Beweis
 Weil jede stetige Funktion
Weil jede stetige Funktion
![$ g:[0,1]\to\mathbb{R}$](img1292.png) mit
beschränkter Variation fast überall differenzierbar ist, ergibt
sich die Behauptung unmittelbar aus
Theorem 2.25.
mit
beschränkter Variation fast überall differenzierbar ist, ergibt
sich die Behauptung unmittelbar aus
Theorem 2.25.

- Beachte
-
- Ein direkter Beweis von Korollar 2.6 kann wie
folgt geführt werden: Es genügt zu zeigen, dass mit
Wahrscheinlichkeit

![$\displaystyle \lim_{n\to\infty}\sum_{i=1}^{2^n} \bigl\vert X_{i t/2^n} - X_{(i-1)t/2^n}\bigr\vert=\infty\qquad\forall\,t\in(0,1]\,.$](img1293.png) |
(42) |
- Um (42) zu beweisen, setzen wir
- Dann gilt
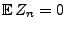 , und außerdem kann man leicht zeigen, dass
, und außerdem kann man leicht zeigen, dass
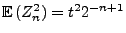 .
.
- Aus der Tschebyschew-Ungleichung (vgl. Abschnitt WR-4.4.3) ergibt
sich, dass für jedes
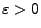 und somit
und somit
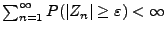 .
.
- Aus dem Lemma von Borel-Cantelli (vgl. Korollar WR-2.3) ergibt
sich nun, dass
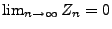 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit
 .
.
- Hieraus folgt, dass mit Wahrscheinlichkeit

- Damit ist die Gültigkeit von (42) bewiesen, weil der
Wiener-Prozess
 stetige Trajektorien hat und weil
deshalb
stetige Trajektorien hat und weil
deshalb




Nächste Seite: Lévy-Prozesse und Martingale
Aufwärts: Wiener-Prozess
Vorherige Seite: Verteilung des Maximums
Inhalt
Ursa Pantle
2005-07-13
![]() , womit die Tatsache gemeint ist,
dass bestimmte Transformationen des Wiener-Prozesses erneut zu
einem Wiener-Prozess führen.
, womit die Tatsache gemeint ist,
dass bestimmte Transformationen des Wiener-Prozesses erneut zu
einem Wiener-Prozess führen.
![$\displaystyle \lim_{n^\prime,m^\prime,k=\infty}
P\Bigl(\bigcap_{n=1}^{n^\prime}...
...up_{t\in\mathbb{Q}_{k}\cap
(0,1/m]}\bigl\{\vert Y_t^{(4)}\vert<1/n\bigr\}\Bigr)$](img1238.png)
![$\displaystyle \lim_{n^\prime,m^\prime,k\to\infty}
P\Bigl(\bigcap_{n=1}^{n^\prim...
...}\sup_{t\in\mathbb{Q}_{k}\cap
(0,1/m]}\bigl\{\vert X_t\vert<1/n\bigr\}\Bigr)\,,$](img1239.png)