Nächste Seite: Weitere Verteilungs- und Pfadeigenschaften
Aufwärts: Wiener-Prozess
Vorherige Seite: Darstellung als Markow-Prozess bzw.
Inhalt
Verteilung des Maximums
In diesem Abschnitt setzen wir die Diskussion von Eigenschaften
des Wiener-Prozesses fort, die mit relativ elementaren
Hilfsmitteln gezeigt werden können. Dabei leiten wir zunächst eine
obere Schranke für die Tailfunktion des Maximums
![$ \max_{t\in[0,1]}
X_t$](img1150.png) von Wiener-Prozessen in
von Wiener-Prozessen in ![$ [0,1]$](img566.png) her.
her.
Später zeigen wir in Kapitel 3 mit den Techniken
von Martingalen bzw. Lévy-Prozessen, dass diese Schranke
,,optimal'' ist, d.h., mit der Tailfunktion von
![$ \max_{t\in[0,1]}
X_t$](img1150.png) übereinstimmt.
übereinstimmt.
- Beachte
-
- Die in (23) betrachtete Abbildung
![$ \max_{t\in[0,1]}
X_t:\Omega\to[0,\infty)$](img1152.png) ist eine wohldefinierte Zufallsvariable,
weil die Trajektorien von
ist eine wohldefinierte Zufallsvariable,
weil die Trajektorien von  stetige Funktionen sind und
somit
stetige Funktionen sind und
somit
![$\displaystyle \bigl(\max_{t\in[0,1]} X_t\bigr)(\omega)=\lim_{k\to\infty}\;\bigl(\max_{i=1,\ldots,k}X_{i/k}\bigr)(\omega) \qquad\forall\,\omega\in\Omega\,.$](img1153.png) |
(24) |
- Aus (23) folgt, dass die Zufallsvariable
![$ \max_{t\in[0,1]}
X_t$](img1150.png) einen exponentiell beschränkten Tail hat.
Hieraus ergibt sich insbesondere, dass sämtliche Momente von
einen exponentiell beschränkten Tail hat.
Hieraus ergibt sich insbesondere, dass sämtliche Momente von
![$ \max_{t\in[0,1]}
X_t$](img1150.png) existieren (und endlich sind).
existieren (und endlich sind).
- Im Beweis von Theorem 2.23 benötigen wir
Bezeichnungen und Hilfsmittel, die teilweise bereits in der
Vorlesung ,,Wahrscheinlichkeitsrechnung'' bereitgestellt wurden.
- Das folgende Lemma zeigt, dass
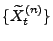 als
Approximation des Wiener-Prozesses
als
Approximation des Wiener-Prozesses  aufgefasst werden
kann.
aufgefasst werden
kann.
- Allerdings konvergiert der in (25) gegebene Prozess
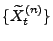 nur ,,in Verteilung'' für
nur ,,in Verteilung'' für
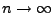 gegen
gegen  ,
,
- während die in Abschnitt 2.4.3 betrachtete
Approximation
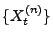 mit
mit
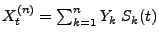 ,,pfadweise'' für
,,pfadweise'' für
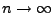 gegen den Wiener-Prozess
gegen den Wiener-Prozess
 konvergiert.
konvergiert.
Lemma 2.9

Für jedes
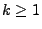
und für beliebige
![$ t_1,\ldots,t_k\in[0,1]$](img1165.png)
gilt
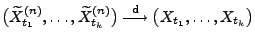 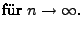 |
(26) |
- Beweis
-
- Beweis
-
- Die Gleichung (27) folgt unmittelbar aus der in
(25) gegebenen Definition von
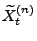 .
.
- Die Gleichung (28) beruht auf dem sogenannten
- Reflexionsprinzip der maximalen Gewinnsume bei
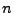 -maligem
Münzwurf
-maligem
Münzwurf
- und wurde bereits in Abschnitt WR-5.3.2 hergeleitet (vgl. Formel
(68) in Abschnitt WR-5.3.2).

- Beweis von Theorem 2.23
-
- Aus Lemma 2.9 ergibt sich, dass für beliebige
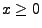 ,
, 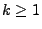 und
und
![$ t_1,\ldots,t_k\in[0,1]$](img1165.png)
- Hieraus folgt, dass
- Mit
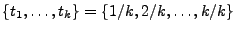 ergibt sich nun
unter Beachtung von (24), dass
ergibt sich nun
unter Beachtung von (24), dass
- Wegen Lemma 2.10 ist damit die Ungleichung
(23) bewiesen.

- Beachte
 Sei
Sei
 ein Wiener-Prozess über
ein Wiener-Prozess über
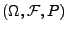 . Dabei setzen wir (wie stets in diesem Skript)
voraus, dass
. Dabei setzen wir (wie stets in diesem Skript)
voraus, dass
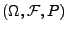 ein vollständiger
Wahrscheinlichkeitsraum ist, d.h.,
ein vollständiger
Wahrscheinlichkeitsraum ist, d.h.,
- dass sämtliche ,,Nullmengen'' des Wahrscheinlichkeitsraumes
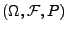 , über dem der Wiener-Prozess
, über dem der Wiener-Prozess  gegeben
ist, zu
gegeben
ist, zu
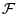 gehören, bzw. (äquivalent hierzu)
gehören, bzw. (äquivalent hierzu)
- für
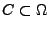 gilt
gilt
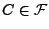 , falls es Teilmengen
, falls es Teilmengen
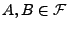 gibt, so dass
gibt, so dass
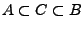 und
und
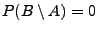 .
.
Aus Theorem 2.23 ergibt sich nun die folgende
asymptotische Eigenschaft des Wiener-Prrozesses.
Korollar 2.4
Sei

ein Wiener-Prozess. Dann gilt mit
Wahrscheinlichkeit

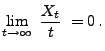 |
(29) |
- Beweis
-




Nächste Seite: Weitere Verteilungs- und Pfadeigenschaften
Aufwärts: Wiener-Prozess
Vorherige Seite: Darstellung als Markow-Prozess bzw.
Inhalt
Ursa Pantle
2005-07-13
![]() von Wiener-Prozessen in
von Wiener-Prozessen in ![]() her.
her.
![]() übereinstimmt.
übereinstimmt.