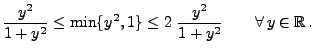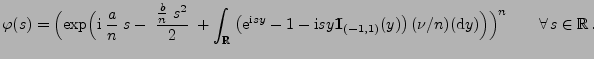Nächste Seite: Lévy-Chintschin-Darstellung
Aufwärts: Lévy-Prozesse
Vorherige Seite: Lévy-Prozesse
Inhalt
Unbegrenzte Teilbarkeit
Wir zeigen zunächst, dass für jeden Lévy-Prozess  und
für jedes
und
für jedes  die Zufallsvariable
die Zufallsvariable 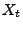 unbegrenzt teilbar
ist, und geben dann in Abschnitt 3.1.2 eine
Darstellungsformel für die charakteristische Funktion von
unbegrenzt teilbar
ist, und geben dann in Abschnitt 3.1.2 eine
Darstellungsformel für die charakteristische Funktion von 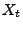 an.
an.
- Definition
 Sei
Sei
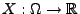 eine beliebige
Zufallsvariable über einem Wahrscheinlichkeitsraum
eine beliebige
Zufallsvariable über einem Wahrscheinlichkeitsraum
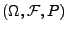 . Man sagt, dass
. Man sagt, dass 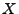 bzw. die Verteilung
bzw. die Verteilung 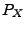 von
von 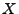 unbegrenzt teilbar ist, wenn es für jedes
unbegrenzt teilbar ist, wenn es für jedes 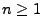 unabhängige und identisch verteilte Zufallsvariablen
unabhängige und identisch verteilte Zufallsvariablen
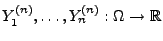 gibt mit
gibt mit
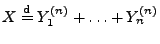 .
.
Theorem 3.1

Sei

ein
Lévy-Prozess. Dann ist die Zufallsvariable
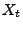
für jedes

unbegrenzt teilbar.
- Beweis
-
Das folgende Lemma enthält ein einfaches (jedoch nützliches)
Hilfsmittel zur Untersuchung von unbegrenzt teilbaren
Zufallsvariablen.
Lemma 3.1

Die Zufallsvariable
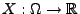
ist genau dann unbegrenzt teilbar, wenn sich die
charakteristische Funktion
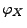
von
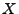
für jedes
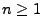
darstellen lässt in der Form
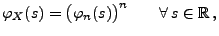 |
(1) |
wobei
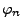
die charakteristische Funktion einer
Zufallsvariablen ist.
- Beweis
-
- Die Notwendigkeit der Bedingung (1) ergibt sich
unmittelbar
- aus der Definition der unbegrenzten Teilbarkeit und aus der
Tatsache, dass
- die charakteristische Funktion der Summe von unabhängigen
Zufallsvariablen gleich dem Produkt der charakteristischen
Funktionen der Summanden ist (vgl. Theorem WR-5.18).
- Es gelte nun umgekehrt (1), und
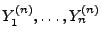 seien unabhängige Zufallsvariablen
mit der charakteristischen Funktion
seien unabhängige Zufallsvariablen
mit der charakteristischen Funktion 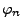 .
.
- Dann ergibt sich durch die erneute Anwendung von Theorem WR-5.18,
dass
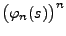 die charakteristische Funktion
der Summe
die charakteristische Funktion
der Summe
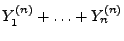 ist.
ist.
- Wegen (1) stimmen also die charakteristischen
Funktionen von
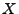 und
und
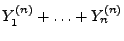 überein.
überein.
- Aus dem Eindeutigkeitssatz für charakteristische Funktionen (vgl.
Korollar WR-5.5) ergibt sich nun, dass auch die Verteilungen von
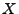 und
und
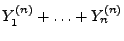 übereinstimen.
übereinstimen.

Wir benötigen noch einen Stetigkeitssatz für charakteristische
Funktionen, der eine (teilweise) Verschärfung von Theorem WR-5.20
ist und den wir hier ohne Beweis angeben.
Lemma 3.2
- Sei
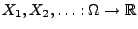 eine beliebige Folge von
Zufallsvariablen, und seien
eine beliebige Folge von
Zufallsvariablen, und seien
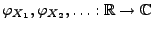 ihre
charakteristischen Funktionen.
ihre
charakteristischen Funktionen.
- Falls es eine Funktion
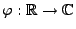 gibt, so dass
gibt, so dass
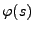 stetig im Punkt
stetig im Punkt 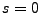 ist und
ist und
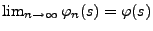 für jedes
für jedes
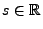 gilt,
gilt,
- dann ist
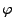 die charakteristische Funktion einer
Zufallsvariablen
die charakteristische Funktion einer
Zufallsvariablen 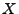 ,
,
- und es gilt
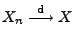 .
.
Außerdem spielt der Begriff des Lévy-Maßes eine wichtige Rolle
bei der Untersuchung von unbegrenzt teilbaren Verteilungen.
- Definition
 Sei
Sei 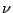 ein Maß über dem Messraum
ein Maß über dem Messraum
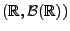 . Man sagt, dass
. Man sagt, dass 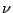 ein Lévy-Maß ist,
wenn
ein Lévy-Maß ist,
wenn
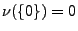 und
und
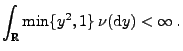 |
(2) |
- Beachte
-
- Man kann sich leicht überlegen, dass jedes Lévy-Maß
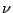 ein
ein
 -endliches Maß ist und dass
-endliches Maß ist und dass
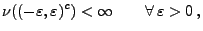 |
(3) |
wobei
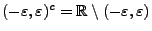 .
.
- Insbesondere ist jedes endliche Maß
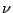 über
über
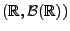 ein Lévy-Maß, falls
ein Lévy-Maß, falls
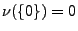 .
.
- Eine zu (2) äquivalente Bedingung ist
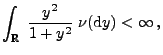 |
(4) |
denn es gilt
Der folgende Ansatz zur Konstruktion charakteristischer Funktionen
von unbegrenzt teilbaren Verteilungen wird in der Literatur die
Lévy-Chintschin-Formel genannt.
Theorem 3.2

Seien
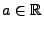
und
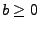
beliebige Konstanten, und sei
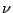
ein beliebiges Lévy-Maß. Dann ist durch die Funktion
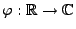
mit
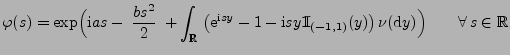 |
(5) |
die charakteristische Funktion einer unbegrenzt teilbaren
Zufallsvariablen gegeben.
- Beweis
-
- Beachte

- Das Tripel
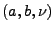 , das in der Lévy-Chintschin-Formel
(5) auftritt, wird Lévy-Charakteristik der
zugehörigen unbegrenzt teilbaren Verteilung genannt.
, das in der Lévy-Chintschin-Formel
(5) auftritt, wird Lévy-Charakteristik der
zugehörigen unbegrenzt teilbaren Verteilung genannt.
- Die Abbildung
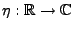 mit
mit
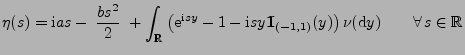 |
(8) |
im Exponent von (5) heißt Lévy-Exponent
dieser unbegrenzt teilbaren Verteilung.




Nächste Seite: Lévy-Chintschin-Darstellung
Aufwärts: Lévy-Prozesse
Vorherige Seite: Lévy-Prozesse
Inhalt
Ursa Pantle
2005-07-13
![]() und
für jedes
und
für jedes ![]() die Zufallsvariable
die Zufallsvariable ![]() unbegrenzt teilbar
ist, und geben dann in Abschnitt 3.1.2 eine
Darstellungsformel für die charakteristische Funktion von
unbegrenzt teilbar
ist, und geben dann in Abschnitt 3.1.2 eine
Darstellungsformel für die charakteristische Funktion von ![]() an.
an.