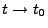Nächste Seite: Unbegrenzte Teilbarkeit
Aufwärts: Lévy-Prozesse und Martingale
Vorherige Seite: Lévy-Prozesse und Martingale
Inhalt
Lévy-Prozesse
In Abschnitt 2.2.2 hatten wir zusammengesetzte
Poisson-Prozesse betrachtet und gezeigt, dass sie unabhängige und
stationäre Zuwächse besitzen (vgl. Theorem 2.10). Der
Wiener-Prozess besitzt ebenfalls diese beiden Eigenschaften, was
sich unmittelbar aus seiner Definition ergibt (vgl.
Abschnitt 2.4).
Wir betrachten nun eine allgemeine Klasse von stochastischen
Prozessen mit unabhängigen und stationären Zuwächsen, die sowohl
zusammengesetzte Poisson-Prozesse als auch den Wiener-Prozess
als Spezialfälle umfasst.
- Definition
 Ein stochastischer Prozess
Ein stochastischer Prozess
 über einem (im
allgemeinen nicht näher spezifizierten) Wahrscheinlichkeitsraum
über einem (im
allgemeinen nicht näher spezifizierten) Wahrscheinlichkeitsraum
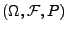 heißt Lévy-Prozess, wenn
heißt Lévy-Prozess, wenn
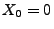 ,
,
 unabhängige und stationäre Zuwächse hat,
unabhängige und stationäre Zuwächse hat,
 stochastisch stetig ist, d.h., für beliebige
stochastisch stetig ist, d.h., für beliebige
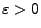 und
und 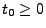 gilt
gilt
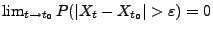 .
.
- Beachte
-
- Man kann sich leicht überlegen, dass für zusammengesetzte
Poisson-Prozesse die dritte Bedingung ebenfalls erfüllt ist. Denn
es gilt dann für jedes
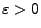 und für
und für 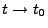 wobei
wobei 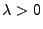 die Intensität der Sprungzeitpunkte bezeichnet.
die Intensität der Sprungzeitpunkte bezeichnet.
- Darüber hinaus gilt auch im Fall des Wiener-Prozesses für jedes
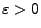 und für
und für 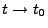
Unterabschnitte




Nächste Seite: Unbegrenzte Teilbarkeit
Aufwärts: Lévy-Prozesse und Martingale
Vorherige Seite: Lévy-Prozesse und Martingale
Inhalt
Ursa Pantle
2005-07-13
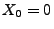 ,
,
 unabhängige und stationäre Zuwächse hat,
unabhängige und stationäre Zuwächse hat,
 stochastisch stetig ist, d.h., für beliebige
stochastisch stetig ist, d.h., für beliebige
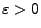 und
und 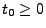 gilt
gilt
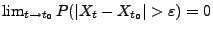 .
.
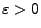 und für
und für 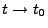 wobei
wobei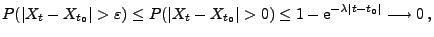
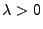 die Intensität der Sprungzeitpunkte bezeichnet.
die Intensität der Sprungzeitpunkte bezeichnet.
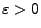 und für
und für