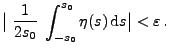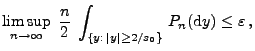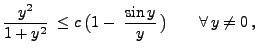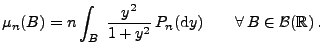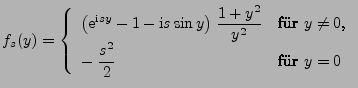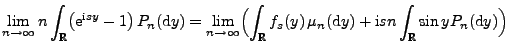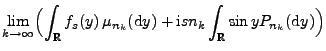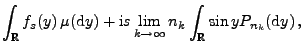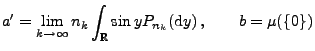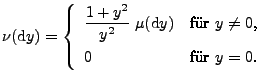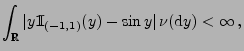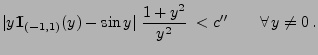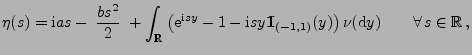Nächste Seite: Beispiele: Wiener-Prozess, zusammengesetzte Poisson-Prozesse,
Aufwärts: Lévy-Prozesse
Vorherige Seite: Unbegrenzte Teilbarkeit
Inhalt
Lévy-Chintschin-Darstellung
In diesem Abschnitt zeigen wir, dass für jeden Lévy-Prozess
 und für jedes
und für jedes  die charakteristische Funktion
der unbegrenzt teilbaren Zufallsvariablen
die charakteristische Funktion
der unbegrenzt teilbaren Zufallsvariablen 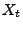 durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann.
durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann.
Dabei zeigen wir zunächst, dass die charakteristische Funktion von
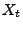 auf einfache Weise durch die charakteristische Funktion
von
auf einfache Weise durch die charakteristische Funktion
von 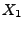 ausgedrückt werden kann. Hierfür benötigen wir den
folgenden Hilfssatz.
ausgedrückt werden kann. Hierfür benötigen wir den
folgenden Hilfssatz.
Lemma 3.3

Sei

ein stochastisch stetiger Prozess, d.h. für
beliebige
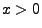
und
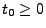
gelte
Dann ist für jedes
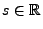
durch
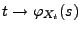
eine
stetige Abbildung von
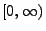
nach
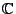
gegeben.
- Beweis
-
Theorem 3.3

Sei

ein
Lévy-Prozess. Dann ist für jedes

die charakteristische
Funktion
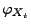
von
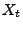
gegeben durch
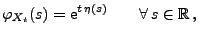 |
(9) |
wobei
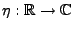
eine stetige Funktion ist. Insbesondere
gilt somit
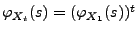
für beliebige
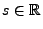
,

.
- Beweis
-
- Weil
 unabhängige und stationäre Zuwächse hat, gilt für
beliebige
unabhängige und stationäre Zuwächse hat, gilt für
beliebige
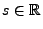 und
und
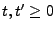
- Für jedes
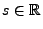 gilt also für die Funktion
gilt also für die Funktion
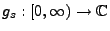 mit
mit
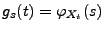 , dass
, dass
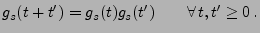 |
(10) |
- Weil
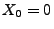 , gilt außerdem für jedes
, gilt außerdem für jedes
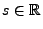
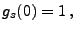 |
(11) |
und in Lemma 3.3 hatten wir gezeigt, dass die
Funktion
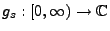 für jedes
für jedes
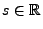 stetig ist.
stetig ist.
- Man kann sich leicht überlegen, dass es für jede Familie von
stetigen Funktionen
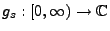 , die den Bedingungen
(10) und (11) genügen, eine Funktion
, die den Bedingungen
(10) und (11) genügen, eine Funktion
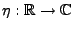 gibt, so dass
gibt, so dass
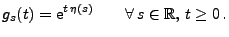 |
(12) |
- Es genügt nun,
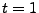 zu setzen, um zu erkennen, dass
zu setzen, um zu erkennen, dass
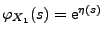 für jedes
für jedes
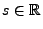 gilt und
dass somit
gilt und
dass somit
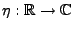 eine stetige Funktion ist.
eine stetige Funktion ist.

Wir zeigen nun, dass für jeden Lévy-Prozess  die
charakteristische Funktion von
die
charakteristische Funktion von 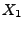 durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann. Hierfür benötigen wir den folgenden Hilfssatz zur
Charakterisierung der relativen Kompaktheit von Familien
(gleichmäßig beschränkter) endlicher Maße.
durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann. Hierfür benötigen wir den folgenden Hilfssatz zur
Charakterisierung der relativen Kompaktheit von Familien
(gleichmäßig beschränkter) endlicher Maße.
Lemma 3.4

Sei
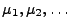
eine
Folge von endlichen Maßen, die über der Borel-

-Algebra
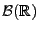
definiert sind. Falls
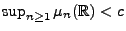
für
ein
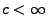
und falls es für jedes
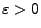
eine
kompakte Menge
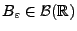
gibt, so dass
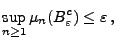 |
(13) |
dann gibt es eine Teilfolge
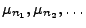
und ein
endliches Maß
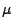
über
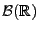
, so dass für jede stetige
und beschränkte Funktion
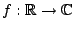
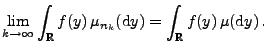 |
(14) |
Der Beweis von Lemma 3.4 geht über den Rahmen
dieser Vorlesung hinaus und wird deshalb weggelassen; er kann
beispielsweise im Buch von A.V. Skorokhod (2005), S. 122-123
nachgelesen werden.
Theorem 3.4

Sei

ein
Lévy-Prozess. Dann gibt es Konstanten
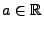
,
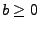
und
ein Lévy-Maß
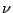
, so dass
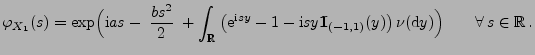 |
(15) |
- Beweis
-
- Aus Theorem 3.3 ergibt sich, dass für jede Nullfolge
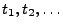 positiver Zahlen
positiver Zahlen
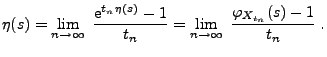 |
(16) |
- Weil
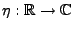 eine stetige Funktion ist, ergibt sich durch
Taylor-Reihenentwicklung der Funktion
eine stetige Funktion ist, ergibt sich durch
Taylor-Reihenentwicklung der Funktion
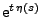 nach
nach
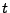 , dass für jedes
, dass für jedes
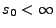 die Konvergenz in
(16) gleichmäßig in
die Konvergenz in
(16) gleichmäßig in
![$ s\in[-s_0,s_0]$](img1401.png) erfolgt.
erfolgt.
- Wir setzen nun
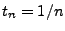 und bezeichnen die Verteilung von
und bezeichnen die Verteilung von
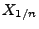 mit
mit 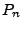 . Mit dieser Schreibweise gilt
. Mit dieser Schreibweise gilt
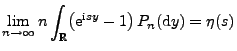 |
(17) |
gleichmäßig in
![$ s\in[-s_0,s_0]$](img1401.png) .
.
- Wenn auf beiden Seiten dieser Gleichung über
![$ s\in[-s_0,s_0]$](img1401.png) integriert wird,
integriert wird,
- dann ergibt sich aus dem Satz von Lebesgue über die majorisierte
Konvergenz (und nach Vertauschung der Integrationsreihenfolge auf
der linken Seite), dass für jedes
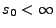
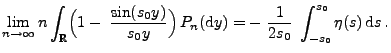 |
(18) |
- Weil
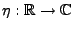 eine stetige Funktion ist mit
eine stetige Funktion ist mit 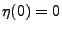 ,
gibt es für jedes
,
gibt es für jedes
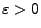 ein
ein 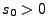 , so dass
, so dass
- Weil außerdem
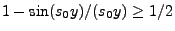 für
für
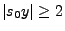 ,
ergibt sich somit aus (18),
,
ergibt sich somit aus (18),
- dass es für jedes
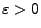 ein
ein 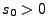 gibt, so dass
gibt, so dass
- bzw. dass es für jedes
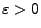 ein
ein 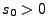 und ein
und ein 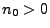 gibt, so dass
gibt, so dass
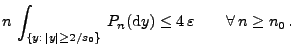 |
(19) |
- Wir verkleinern nun
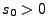 weiter (falls erforderlich), so dass
die Ungleichung in (19) auch für jedes
weiter (falls erforderlich), so dass
die Ungleichung in (19) auch für jedes
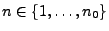 gilt.
gilt.
- Insgesamt haben wir somit gezeigt, dass es für jedes
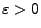 ein
ein 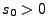 gibt, so dass
gibt, so dass
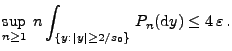 |
(20) |
- Weil es ein
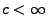 gibt, so dass
ergibt sich aus (18), dass es eine Konstante
gibt, so dass
ergibt sich aus (18), dass es eine Konstante
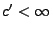 gibt, so dass
gibt, so dass
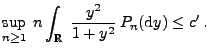 |
(21) |
- Für jedes
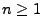 sei das (endliche) Maß
sei das (endliche) Maß
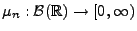 gegeben durch
gegeben durch
- Weil für jedes
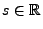 die Funktion
die Funktion
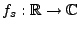 mit
stetig und beschränkt ist, ergibt sich aus (17) und
(22), dass
mit
stetig und beschränkt ist, ergibt sich aus (17) und
(22), dass
wobei sich die Existenz und Endlichkeit des letzten Grenzwertes
aus der Tatsache ergibt, das alle übrigen Grenzwerte in dieser
Gleichungskette existieren und endlich sind.
- Hieraus folgt, dass
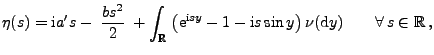 |
(23) |
wobei
und das Lévy-Maß
![$ \nu:\mathcal{B}(\mathbb{R})\to[0,\infty]$](img1431.png) gegeben ist durch
gegeben ist durch
- Außerdem gilt
weil es eine Konstante
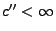 gibt, so dass
gibt, so dass
- Aus (23) ergibt sich somit, dass
wobei
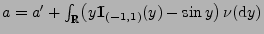 .
.

Korollar 3.1

Sei

ein
Lévy-Prozess. Dann sind sämtliche endlich-dimensionalen
Verteilungen von

eindeutig durch die
Lévy-Charakteristik
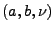
von
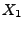
bestimmt.
- Beweis
-
- Aus den Theoremen 3.3 und 3.4 ergibt
sich zusammen mit dem Eindeutigkeitssatz für charakteristische
Funktionen (vgl. Korollar WR-5.5), dass die Verteilung von
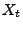 für jedes
für jedes  eindeutig durch die Lévy-Charakteristik
eindeutig durch die Lévy-Charakteristik
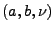 von
von 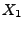 bestimmt ist.
bestimmt ist.
- Weil
 unabhängige und stationäre Zuwächse hat, sind damit
auch sämtliche endlich-dimensionalen Verteilungen von
unabhängige und stationäre Zuwächse hat, sind damit
auch sämtliche endlich-dimensionalen Verteilungen von  eindeutig durch die Lévy-Charakteristik von
eindeutig durch die Lévy-Charakteristik von 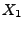 bestimmt.
bestimmt.





Nächste Seite: Beispiele: Wiener-Prozess, zusammengesetzte Poisson-Prozesse,
Aufwärts: Lévy-Prozesse
Vorherige Seite: Unbegrenzte Teilbarkeit
Inhalt
Ursa Pantle
2005-07-13
![]() und für jedes
und für jedes ![]() die charakteristische Funktion
der unbegrenzt teilbaren Zufallsvariablen
die charakteristische Funktion
der unbegrenzt teilbaren Zufallsvariablen ![]() durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann.
durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann.
![]() auf einfache Weise durch die charakteristische Funktion
von
auf einfache Weise durch die charakteristische Funktion
von ![]() ausgedrückt werden kann. Hierfür benötigen wir den
folgenden Hilfssatz.
ausgedrückt werden kann. Hierfür benötigen wir den
folgenden Hilfssatz.
![]() die
charakteristische Funktion von
die
charakteristische Funktion von ![]() durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann. Hierfür benötigen wir den folgenden Hilfssatz zur
Charakterisierung der relativen Kompaktheit von Familien
(gleichmäßig beschränkter) endlicher Maße.
durch die
Lévy-Chintschin-Formel (5) dargestellt werden
kann. Hierfür benötigen wir den folgenden Hilfssatz zur
Charakterisierung der relativen Kompaktheit von Familien
(gleichmäßig beschränkter) endlicher Maße.