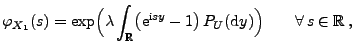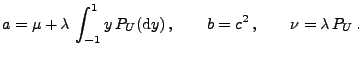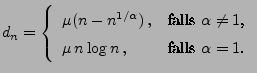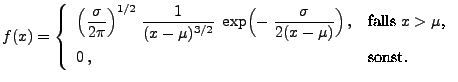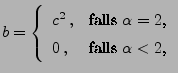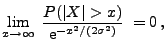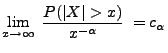Nächste Seite: Subordinatoren
Aufwärts: Lévy-Prozesse
Vorherige Seite: Lévy-Chintschin-Darstellung
Inhalt
Beispiele: Wiener-Prozess, zusammengesetzte Poisson-Prozesse,
stabile Lévy-Prozesse
Bereits am Anfang von Abschnitt 3.1 hatten wir
gezeigt, dass sowohl der Wiener-Prozess als auch beliebige
zusammengesetzte Poisson-Prozesse den drei Bedingungen in der
Definition von Lévy-Prozessen genügen.
Wir bestimmen nun die Lévy-Charakteristik 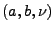 für diese
und weitere Beispiele von Lévy-Prozessen.
für diese
und weitere Beispiele von Lévy-Prozessen.
 Wiener-Prozess (mit Drift)
Wiener-Prozess (mit Drift)
 zusammengesetzte Poisson-Prozesse
zusammengesetzte Poisson-Prozesse
 Lévy-Prozesse vom Gauß-Poisson-Typ
Lévy-Prozesse vom Gauß-Poisson-Typ
 stabile Lévy-Prozesse
stabile Lévy-Prozesse
- Eine wichtige Eigenschaft der Normalverteilung ist ihre
Faltungsstabilität (vgl. Korollar WR-3.2), die sich wie folgt
charakterisieren lässt:
- Die Faltungsgleichung (25) lässt sich auf die
folgende Weise verallgemeinern.
- Man kann zeigen, dass für jedes
![$ \alpha\in(0,2]$](img1468.png) eine Lösung der
(verallgemeinerten) Faltungsgleichung (26)
existiert, vgl. Samorodnitsky und Taqqu (1994) bzw. K.-I. Sato
(1999). Dabei gilt für ein
eine Lösung der
(verallgemeinerten) Faltungsgleichung (26)
existiert, vgl. Samorodnitsky und Taqqu (1994) bzw. K.-I. Sato
(1999). Dabei gilt für ein
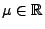
- Neben dem klassischen Fall
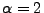 , der zur Normalverteilung
führt, gibt es weitere wohlbekannte Beispiele stabiler
Verteilungen, für die man zeigen kann, dass sie der Gleichung
(26) genügen. Und zwar
, der zur Normalverteilung
führt, gibt es weitere wohlbekannte Beispiele stabiler
Verteilungen, für die man zeigen kann, dass sie der Gleichung
(26) genügen. Und zwar
- Es ist klar, dass die Faltungsgleichung (26) genau
dann gilt, wenn
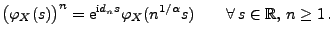 |
(27) |
- Wenn
 (wie beispielsweise bei der Cauchy-Verteilung
mit
(wie beispielsweise bei der Cauchy-Verteilung
mit 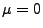 ),
),
- Außerdem kann man zeigen, dass für jede stabile Zufallsvariable
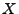 die Charakteristik
die Charakteristik 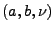 in der
Lévy-Chintschin-Darstellung (5) von
in der
Lévy-Chintschin-Darstellung (5) von 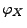 gegeben ist durch eine (beliebige) reelle Zahl
gegeben ist durch eine (beliebige) reelle Zahl
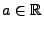 ,
und
,
und
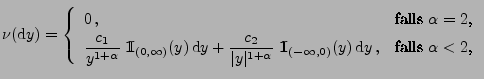 |
(29) |
wobei 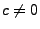 und
und
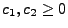 gewisse Konstanten sind mit
gewisse Konstanten sind mit
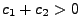 .
.
- Die Tails von stabilen Zufallsvariablen können entweder
exponentiell beschränkt sein (für
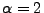 ) oder polynomial
abklingen (für
) oder polynomial
abklingen (für 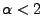 ):
):
- Wenn
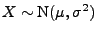 , d.h.,
, d.h., 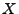 hat eine
stabile Verteilung mit Stabilitätsindex
hat eine
stabile Verteilung mit Stabilitätsindex 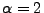 , dann gilt
d.h.,
, dann gilt
d.h., 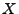 hat sogenannte ,,leichte'' (exponentiell beschränkte)
Tails.
hat sogenannte ,,leichte'' (exponentiell beschränkte)
Tails.
- Wenn
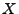 dagegen eine stabile Zufallsvariable mit Stabilitätsindex
dagegen eine stabile Zufallsvariable mit Stabilitätsindex
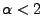 ist, dann kann man zeigen, dass
für ein
ist, dann kann man zeigen, dass
für ein
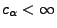 , d.h.,
, d.h., 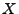 hat ,,schwere'' (polynomial
abklingende) Tails.
hat ,,schwere'' (polynomial
abklingende) Tails.
- Beachte: Der Lévy-Prozess
 heißt stabiler
Lévy-Prozess, falls
heißt stabiler
Lévy-Prozess, falls 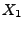 eine stabile Verteilung hat.
eine stabile Verteilung hat.




Nächste Seite: Subordinatoren
Aufwärts: Lévy-Prozesse
Vorherige Seite: Lévy-Chintschin-Darstellung
Inhalt
Ursa Pantle
2005-07-13
![]() für diese
und weitere Beispiele von Lévy-Prozessen.
für diese
und weitere Beispiele von Lévy-Prozessen.