



Nächste Seite: Ungleichung von Doob
Aufwärts: Martingale
Vorherige Seite: Submartingale und Supermartingale; Beispiele
Inhalt
Gleichgradige Integrierbarkeit
Sei 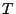 eine endliche Stoppzeit, und der stochastische Prozess
eine endliche Stoppzeit, und der stochastische Prozess
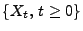 sei càdlàg mit
sei càdlàg mit
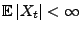 für jedes
für jedes
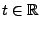 . In Korollar 3.2 hatten wir gezeigt, dass
dann
. In Korollar 3.2 hatten wir gezeigt, dass
dann 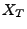 eine wohldefinierte Zufallsvariable ist.
eine wohldefinierte Zufallsvariable ist.
Zur Herleitung von Bedingungen, so dass auch
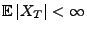 gilt, benötigen wir den Begriff der gleichgradigen
Integrierbarkeit von Zufallsvariablen.
gilt, benötigen wir den Begriff der gleichgradigen
Integrierbarkeit von Zufallsvariablen.
Hierfür benutzen wir die folgende Schreibweise: Sei
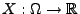 eine beliebige Zufallsvariable mit
eine beliebige Zufallsvariable mit
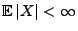 . Für jedes
. Für jedes
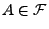 setzen wir dann
setzen wir dann
![$ {\mathbb{E}\,}[X;A]={\mathbb{E}\,}(X{1\hspace{-1mm}{\rm I}}(A))$](img1718.png) .
.
- Definition
 Die Folge
Die Folge
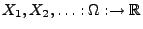 von
Zufallsvariablen heißt gleichgradig integrierbar, wenn
von
Zufallsvariablen heißt gleichgradig integrierbar, wenn
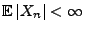 für jedes
für jedes 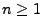 und
und
![$\displaystyle \lim_{x\to\infty}\bigl(\sup_{n\ge 1} {\mathbb{E}\,}[\vert X_n\vert; \vert X_n\vert>x]\bigr)=0\,.$](img1721.png) |
(14) |
- Beweis

- Wir zeigen zuerst, dass (14) gilt, wenn die
Bedingungen (i) und (ii) erfüllt sind.
- Sei nun
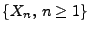 gleichgradig integrierbar.
gleichgradig integrierbar.
Die Bedeutung der gleichgradigen Integrierbarkeit für die
Konvergenz von Zufallsvariablen wird durch das folgende Lemma
deutlich.
Lemma 3.7
Sei
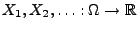
eine beliebige Folge von
Zufallsvariablen mit
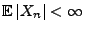
für jedes
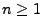
und
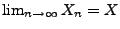
mit Wahrscheinlichkeit
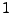
für eine
gewisse Zufallsvariable
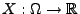
. Dann sind die beiden
folgenden Aussagen äquivalent:
(a)
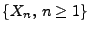
ist gleichgradig integrierbar.
(b)
Es gilt
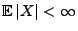
und
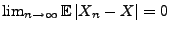
.
- Beweis

Korollar 3.3
Sei
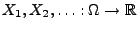
eine Folge von Zufallsvariablen,
so dass
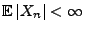
für jedes
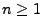
und
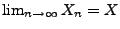
mit Wahrscheinlichkeit
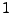
. Wenn
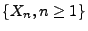
gleichgradig integrierbar ist, dann gilt
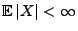
und
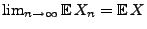
.
- Beweis
 Wegen
Wegen
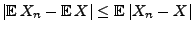 ergibt
sich die Behauptung unmittelbar aus Lemma 3.7.
ergibt
sich die Behauptung unmittelbar aus Lemma 3.7.





Nächste Seite: Ungleichung von Doob
Aufwärts: Martingale
Vorherige Seite: Submartingale und Supermartingale; Beispiele
Inhalt
Ursa Pantle
2005-07-13
![]() eine endliche Stoppzeit, und der stochastische Prozess
eine endliche Stoppzeit, und der stochastische Prozess
![]() sei càdlàg mit
sei càdlàg mit
![]() für jedes
für jedes
![]() . In Korollar 3.2 hatten wir gezeigt, dass
dann
. In Korollar 3.2 hatten wir gezeigt, dass
dann ![]() eine wohldefinierte Zufallsvariable ist.
eine wohldefinierte Zufallsvariable ist.
![]() gilt, benötigen wir den Begriff der gleichgradigen
Integrierbarkeit von Zufallsvariablen.
gilt, benötigen wir den Begriff der gleichgradigen
Integrierbarkeit von Zufallsvariablen.
![]() eine beliebige Zufallsvariable mit
eine beliebige Zufallsvariable mit
![]() . Für jedes
. Für jedes
![]() setzen wir dann
setzen wir dann
![]() .
.