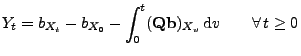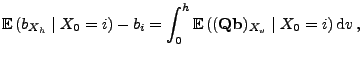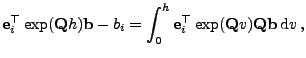- Der Prozess
 sei adaptiert, und es gelte
sei adaptiert, und es gelte
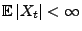 für jedes
für jedes  .
.
- Man sagt, dass
 ein Martingal ist, wenn
ein Martingal ist, wenn
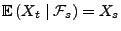 für beliebige
für beliebige 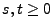 mit
mit 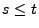 ,
wobei
,
wobei
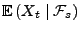 die bedingte Erwartung von
die bedingte Erwartung von 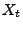 bezüglich der
bezüglich der  -Algebra
-Algebra
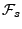 bezeichnet; vgl.
Abschnitt 2.2.3.
bezeichnet; vgl.
Abschnitt 2.2.3.
- Außerdem sagt man, dass
 ein Submartingal bzw. Supermartingal ist, wenn
ein Submartingal bzw. Supermartingal ist, wenn
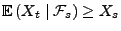 bzw.
bzw.
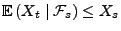 für beliebige
für beliebige 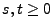 mit
mit 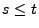 .
.
 Poisson-Prozess
Poisson-Prozess
- Sei
 ein (homogener) Poisson-Prozess mit der
Intensität
ein (homogener) Poisson-Prozess mit der
Intensität 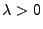 .
.
- Dann kann man sich leicht überlegen, dass der stochastische
Prozess
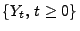 mit
mit
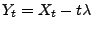 ein Martingal
bezüglich der (natürlichen) Filtration
ein Martingal
bezüglich der (natürlichen) Filtration
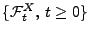 ist.
ist.
- Aus der Unabhängigkeit und Stationarität der Zuwächse von
 und aus den Teilaussagen 4 und 6 von
Theorem 2.11 ergibt sich nämlich, dass
und aus den Teilaussagen 4 und 6 von
Theorem 2.11 ergibt sich nämlich, dass
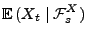
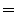
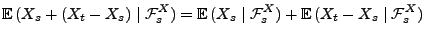
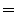
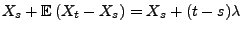
für beliebige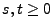 mit
mit 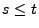 ,
,
- d.h.,
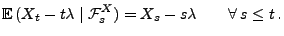
- Aus der Unabhängigkeit und Stationarität der Zuwächse von
- Außerdem kann man zeigen, dass der stochastische Prozess
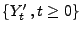 mit
mit
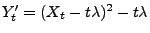 ein Martingal ist.
ein Martingal ist.
- Sei
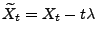 .
.
- Dann ergibt sich aus der Unabhängigkeit der Zuwächse von
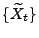 und aus den Eigenschaften der bedingten
Erwartung (vgl. Theorem 2.11), dass für beliebige
und aus den Eigenschaften der bedingten
Erwartung (vgl. Theorem 2.11), dass für beliebige
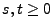 mit
mit 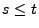
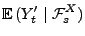
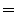
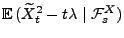
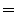
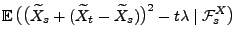
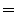
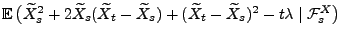
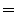
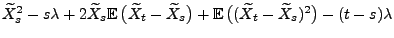
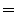
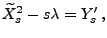
- wobei in der vorletzten Gleichheit die Tatsache genutzt wurde,
dass
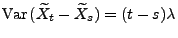 .
.
- Sei
- Sei
 zusammengesetzte Poisson-Prozesse
zusammengesetzte Poisson-Prozesse
- Sei
 ein zusammengesetzter Poisson-Prozess mit
den Charakteristiken
ein zusammengesetzter Poisson-Prozess mit
den Charakteristiken
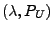 , wobei
, wobei 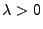 die
Intensität der Sprungzeitpunkte und
die
Intensität der Sprungzeitpunkte und 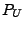 die Verteilung der
Sprunghöhen bezeichnet.
die Verteilung der
Sprunghöhen bezeichnet.
- Wenn die zusätzliche Integrierbarkeitsbedingung
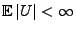 erfüllt ist, dann ist der stochastische Prozess
erfüllt ist, dann ist der stochastische Prozess
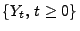 mit
mit
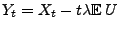 ein Martingal.
ein Martingal.
- Denn genauso wie in dem oben diskutierten Fall des (nicht
zusammengesetzten) Poisson-Prozesses ergibt sich, dass
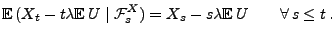
- Sei
 Wiener-Prozess
Wiener-Prozess
- Sei
 ein Wiener-Prozess. Dann kann man auf die
gleiche Weise wie bei den beiden vorhergehenden Beispielen zeigen,
dass
ein Wiener-Prozess. Dann kann man auf die
gleiche Weise wie bei den beiden vorhergehenden Beispielen zeigen,
dass  ein Martingal bezüglich der natürlichen Filtration
ein Martingal bezüglich der natürlichen Filtration
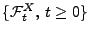 dieses Prozesses ist.
dieses Prozesses ist.
- Außerdem kann man zeigen, dass auch die stochstischen Prozesse
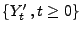 und
und
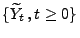 Martingale sind, wobei
und
Martingale sind, wobei
und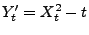 bzw.
bzw.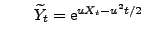
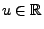 eine beliebige (jedoch fixierte) Zahl ist.
eine beliebige (jedoch fixierte) Zahl ist.
- Denn genauso wie im Poisson-Fall ergibt sich, dass für beliebige
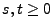 mit
mit 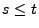 weil
weil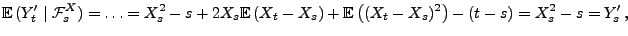
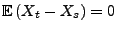 und
und
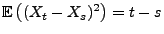 , d.h.,
, d.h.,
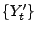 ist ein Martingal.
ist ein Martingal.
- Auf ähnliche Weise ergibt sich, dass für beliebige
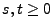 mit
mit
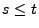 woaus folgt, dass
woaus folgt, dass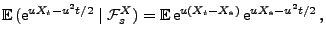
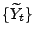 ein Martingale ist, weil
ein Martingale ist, weil
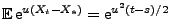 .
.
- Sei
 Lévy-Prozesse
Lévy-Prozesse
- Genauso wie bei den ersten drei Beispielen lässt sich für jeden
Lévy-Prozess
 mit
mit
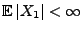 ein
Martingal konstruieren.
ein
Martingal konstruieren.
- Denn für beliebige
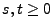 mit
mit 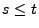 gilt
gilt
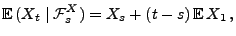
- d.h.,
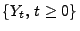 mit
mit
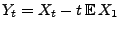 ist ein
Martingal bezüglich der Filtration
ist ein
Martingal bezüglich der Filtration
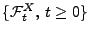 .
.
- Denn für beliebige
- Im allgemeinen, d.h., wenn
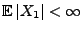 nicht vorausgesetzt
wird, ist für jedes
nicht vorausgesetzt
wird, ist für jedes
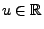 ein (komplexwertiges) Martingal
ein (komplexwertiges) Martingal
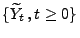 gegeben durch
wobei
gegeben durch
wobei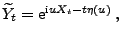
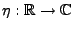 der Lévy-Exponent von
der Lévy-Exponent von  ist; vgl.
die Formel (8) in Abschnitt 3.1.
ist; vgl.
die Formel (8) in Abschnitt 3.1.
- Genauso wie bei den ersten drei Beispielen lässt sich für jeden
Lévy-Prozess
 Markow-Prozesse
Markow-Prozesse
- Wir zeigen nun, wie Martingale für Funktionen von
Markow-Prozessen (mit endlich vielen Zuständen) konstruiert
werden können.
- Sei also
 ein Markow-Prozess mit Werten in der
Menge
ein Markow-Prozess mit Werten in der
Menge
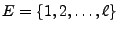 ,
,
- und sei
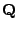 die in Abschnitt 2.3.2 eingeführte
Intensitätsmatrix von
die in Abschnitt 2.3.2 eingeführte
Intensitätsmatrix von  .
.
- Sei also
- Für jeden Vektor
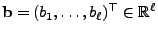 ist
dann der stochastische Prozess
ist
dann der stochastische Prozess
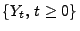 mit
mit
ein Martingal, wobei das Integral in (8) pfadweise gebildet wird.- Weil
 ein homogener Markow-Prozess ist, gilt für
beliebige
ein homogener Markow-Prozess ist, gilt für
beliebige 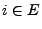 und
und 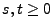 mit
mit 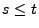
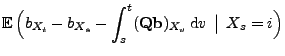
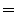
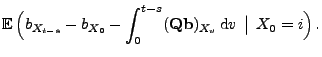
- Um zu zeigen, dass der in (8) gegebene Prozess
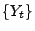 ein Martingal ist, genügt es also zu zeigen, dass für
beliebige
ein Martingal ist, genügt es also zu zeigen, dass für
beliebige 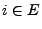 und
und 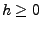
denn man kann sich leicht überlegen, dass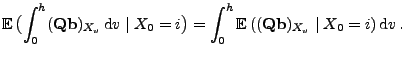
- In Theorem 2.17 hatten wir gezeigt, dass die
Übergangsfunktion
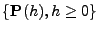 des Markow-Prozesse
des Markow-Prozesse
 für jedes
für jedes 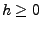 durch
durch
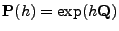 gegeben
ist.
gegeben
ist.
- Hieraus folgt, dass
und
wobei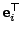 ein
ein 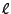 -dimensionaler (Zeilen-) Vektor
ist, für den sämtliche Komponenten gleich 0 sind, bis auf die
-dimensionaler (Zeilen-) Vektor
ist, für den sämtliche Komponenten gleich 0 sind, bis auf die
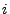 -te Komponente, die gleich
-te Komponente, die gleich  ist.
ist.
- Aus (10) und (11) ergibt sich nun, dass
(9) äquivalent ist mit
wobei sich die Gültigkeit dieser Gleichung aus Lemma 2.3 ergibt, wenn auf beiden Seiten von (12) die Ableitung nach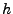 gebildet wird.
gebildet wird.
- Weil
- Wir zeigen nun, wie Martingale für Funktionen von
Markow-Prozessen (mit endlich vielen Zuständen) konstruiert
werden können.
 abgeschlossene Martingale
abgeschlossene Martingale
- Sei
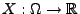 eine beliebige Zufallsvariable mit
eine beliebige Zufallsvariable mit
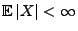 , und sei
, und sei
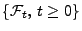 eine beliebige
Filtration.
eine beliebige
Filtration.
- Dann kann man sich leicht überlegen, dass der stochastische
Prozess
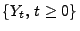 mit
mit
ein Martingal ist, denn aus Teilaussage 6 von Theorem 2.11 ergibt sich, dass für beliebige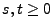 mit
mit 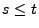
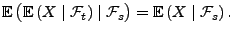
- Manchmal sagt man, dass der in (13) gegebene stochastische Prozess ein abgeschlossenes Martingal ist.
- Sei
- Für die Martingale
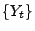 und
und
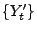 , die in den
Beispielen 1 - 4 betrachtet wurden, gilt
, die in den
Beispielen 1 - 4 betrachtet wurden, gilt
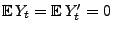 für jedes
für jedes  . Ein Martingal mit dieser
Eigenschaft wird ein zentriertes Martingal genannt.
. Ein Martingal mit dieser
Eigenschaft wird ein zentriertes Martingal genannt.
- Für die Martingale
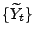 , die in den Beispielen 3
und 4 betrachtet wurden, gilt dagegen
, die in den Beispielen 3
und 4 betrachtet wurden, gilt dagegen
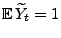 für
jedes
für
jedes  .
.
- Die Definitionsgleichung (8) des Martingals
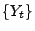 in Beispiel 5 wird Dynkin-Formel für
Markow-Prozesse genannt.
in Beispiel 5 wird Dynkin-Formel für
Markow-Prozesse genannt.