Nächste Seite: Anwendungsbeispiele
Aufwärts: Martingale
Vorherige Seite: Gestoppte Martingale
Inhalt
Optionales Sampling-Theorem
Für jede endliche Stoppzeit
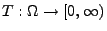 betrachten wir
die
betrachten wir
die  -Algebra
-Algebra
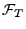 , die gegeben ist durch
, die gegeben ist durch
wobei die folgenden Eigenschaften der ,,gestoppten''
 -Algebra
-Algebra
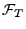 nützlich sind.
nützlich sind.
Lemma 3.9
Für beliebige endliche Stoppzeiten
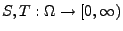
mit
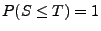
gilt
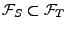
. Außerdem gilt für
jeden adaptierten càdlàg Prozess

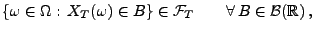 |
(23) |
d.h.,
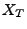
ist eine
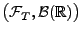
-messbare
Zufallsvariable.
- Beweis

- Wir zeigen zunächst, dass
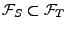 , wenn
, wenn
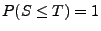 .
.
- Wir zeigen nun, dass
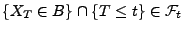 für
beliebige
für
beliebige
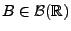 und
und  .
.
Wir kommen nun zum sogenannten optionalen Sampling-Theorem
für Martingale bzw. für gestoppte Martingale.
Theorem 3.12
Der Prozess

sei adaptiert und càdlàg. Wenn

ein Martingal und
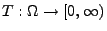
eine endliche
Stoppzeit ist, dann gilt
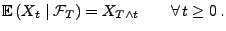 |
(26) |
- Beweis

Korollar 3.4

Der Prozess

sei adaptiert und càdlàg. Wenn

ein Martingal und
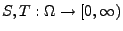
beliebige
endliche Stoppzeiten mit
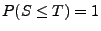
sind, dann gilt
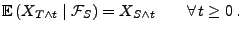 |
(28) |
Insbesondere gilt
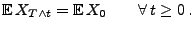 |
(29) |
- Beweis

- Sei
 ein Martingal. Aus Theorem 3.11 folgt
dann, dass der stochastische Prozess
ein Martingal. Aus Theorem 3.11 folgt
dann, dass der stochastische Prozess
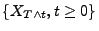 ebenfalls ein Martingal ist.
ebenfalls ein Martingal ist.
- Wenn wir die ,,Stoppzeit''
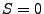 in (28) einsetzen,
dann ergibt sich, dass
in (28) einsetzen,
dann ergibt sich, dass
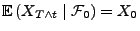 bzw.
bzw.
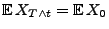 für jedes
für jedes  .
.





Nächste Seite: Anwendungsbeispiele
Aufwärts: Martingale
Vorherige Seite: Gestoppte Martingale
Inhalt
Ursa Pantle
2005-07-13
![]() betrachten wir
die
betrachten wir
die ![]() -Algebra
-Algebra
![]() , die gegeben ist durch
, die gegeben ist durch
![$\displaystyle X_s(\omega)=X_0(\omega){1\hspace{-1mm}{\rm I}}_{\{0\}}(s)+\lim_{n...
...^{2^n}
{1\hspace{-1mm}{\rm I}}_{((k-1)t/2^n,\,kt/2^n]}(s)X_{kt/2^n}(\omega)\,.
$](img1836.png)