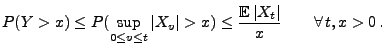Gestoppte Martingale

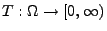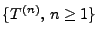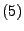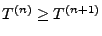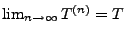Der Prozess $\{X_t,\,t\ge 0\}$ sei adaptiert und c�dl�g. Au�erdem sei $T:\Omega\to[0,\infty)$ eine endliche Stoppzeit und sei $\{T^{(n)},\,n\ge 1\}$ die in $% latex2html id marker 34727 $ (\ref{disc.meth.st})$$ eingef�hrte Folge von diskreten Stoppzeiten mit $T^{(n)}\ge T^{(n+1)}$ und $\lim_{n\to\infty} T^{(n)}=T$ .
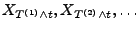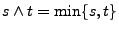Wenn $\{X_t\}$ ein Martingal ist, dann ist die Folge $X_{T^{(1)}\land t},X_{T^{(2)}\land t},\ldots$ gleichgradig integrierbar f�r jedes $t\ge 0$ , wobei $s\land t=\min\{s,t\}$ .

$\displaystyle {\sup_{n\ge 1}{\mathbb{E}\,}[\vert X_{T^{(n)}\land t}\vert; \vert X_{T^{(n)}\land t}\vert>x]}$
	$\displaystyle =$	$\displaystyle \sup_{n\ge 1}\Bigl(\sum_{\{k:\,k<2^nt\}}{\mathbb{E}\,}[\vert X_{k/2^n}\vert; \{T^{(n)}=\frac{k}{2^n}\}\cap\{ \vert X_{T^{(n)}\land t}\vert>x\}]$
		$\displaystyle \hspace{5cm} +{\mathbb{E}\,}[\vert X_t\vert; \{T^{(n)}\ge t\}\cap\{ \vert X_{T^{(n)}\land t}\vert>x\}] \Bigr)$
	$\displaystyle \le$	$\displaystyle \sup_{n\ge 1}\Bigl(\sum_{\{k:\,k<2^nt\}}{\mathbb{E}\,}[\vert X_t\vert; \{T^{(n)}=\frac{k}{2^n}\}\cap\{ \vert X_{T^{(n)}\land t}\vert>x\}]$
		$\displaystyle \hspace{5cm} +{\mathbb{E}\,}[\vert X_t\vert; \{T^{(n)}\ge t\}\cap\{ \vert X_{T^{(n)}\land t}\vert>x\}] \Bigr)$
	$\displaystyle =$	$\displaystyle \sup_{n\ge 1}{\mathbb{E}\,}[\vert X_t\vert; \vert X_{T^{(n)}\land... ...[\left\vert X_t\right\vert; Y> x\right]= {\mathbb{E}\,}[\vert X_t\vert;Y> x]\,,$

$\displaystyle P(Y> x)\le P(\sup_{0\le v\le t}\vert X_v\vert> x)\le \frac{{\mathbb{E}\,}\vert X_t\vert}{x}\qquad\forall\,t,x>0\,.$

$\displaystyle \lim_{x\to\infty} \sup_{n\ge 1}{\mathbb{E}\,}[\vert X_{T^{(n)}\la... ...and t}\vert>x]\le \lim_{x\to\infty} {\mathbb{E}\,}[\vert X_t\vert;Y\ge x]=0\,.$

Theorem 3.11 Der Prozess $\{X_t,\,t\ge 0\}$ sei adaptiert und c�dl�g. Wenn $\{X_t\}$ ein Martingal und $T:\Omega\to[0,\infty)$ eine endliche Stoppzeit ist, dann ist auch der stochastische Prozess $\{X_{T\land t},t\ge 0\}$ ein Martingal.

$\displaystyle {\mathbb{E}\,}\vert X_{T\land t}\vert<\infty$ und $\displaystyle \qquad {\mathbb{E}\,}[X_{T\land t};A]={\mathbb{E}\,}[X_{T\land v};A]\,.$

(20)

$\displaystyle {\mathbb{E}\,}\vert X_{T^{(n)}\land t}\vert<\infty$ und $\displaystyle \qquad {\mathbb{E}\,}[X_{T^{(n)}\land t};A]={\mathbb{E}\,}[X_{T^{(n)}\land v};A]\,.$

(21)

$\displaystyle { {\mathbb{E}\,}(X_{T^{(n)}\land t}\mid\mathcal{F}_v) ={\mathbb{E... ...\mathbb{E}\,}(X_{T^{(n)}\land t}\mid\mathcal{F}_{t_k})\mid\mathcal{F}_v\bigr) }$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( {\mathbb{E}\,}({1\hspace{-1mm}{\rm I}}(T^{(n)}\le... ...rm I}}(T^{(n)}> t_k)X_{T^{(n)}\land t} \mid\mathcal{F}_{t_k})\mid\mathcal{F}_v)$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( {1\hspace{-1mm}{\rm I}}(T^{(n)}\le t_k){\mathbb{E... ...rm I}}(T^{(n)}> t_k){\mathbb{E}\,}(X_t \mid\mathcal{F}_{t_k})\mid\mathcal{F}_v)$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( {1\hspace{-1mm}{\rm I}}(T^{(n)}\le t_k) X_{T^{(n)... ...{\mathbb{E}\,}( {1\hspace{-1mm}{\rm I}}(T^{(n)}> t_k) X_{t_k}\mid\mathcal{F}_v)$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( {1\hspace{-1mm}{\rm I}}(T^{(n)}\le t_k) X_{T^{(n)... ...}( {1\hspace{-1mm}{\rm I}}(T^{(n)}> t_k) X_{T^{(n)}\land t_k}\mid\mathcal{F}_v)$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( X_{T^{(n)}\land t_k} \mid\mathcal{F}_v)$
	$\displaystyle \vdots$
	$\displaystyle =$	$\displaystyle {\mathbb{E}\,}( X_{T^{(n)}\land t_1} \mid\mathcal{F}_v)= {\mathbb{E}\,}( X_{T^{(n)}\land v} \mid\mathcal{F}_v)=X_{T^{(n)}\land v} \,.$