



Nächste Seite: Modifikationen von càdlàg Prozessen
Aufwärts: Einleitung
Vorherige Seite: Endlich-dimensionale Verteilungen; Existenzsatz von
Inhalt
Regularität der Trajektorien
Das folgende Beispiel zeigt, dass der gemäß
Theorem 1.1 zu vorgegebenen Wahrscheinlichkeitsmaßen
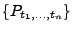 stets existierende stochastische Prozess,
der diese Wahrscheinlichkeitsmaße als endlich-dimensionale
Verteilungen hat, im allgemeinen nicht eindeutig bestimmt
ist.
stets existierende stochastische Prozess,
der diese Wahrscheinlichkeitsmaße als endlich-dimensionale
Verteilungen hat, im allgemeinen nicht eindeutig bestimmt
ist.
- Definition

Ein weiteres Problem besteht darin, dass Teilmengen von
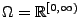 , die durch Eigenschaften der
Trajektorien gegeben sind, im allgemeinen nicht messbar bezüglich
der
, die durch Eigenschaften der
Trajektorien gegeben sind, im allgemeinen nicht messbar bezüglich
der  -Algebra
-Algebra
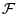 sein müssen, die durch die
Zylinder-Mengen in (4) erzeugt wird.
sein müssen, die durch die
Zylinder-Mengen in (4) erzeugt wird.
Die im folgenden Kapitel 2 betrachteten
klassischen Beispiele von stochastischen Prozessen zeigen jedoch,
dass es nicht ausreicht, nur Prozesse mit stetigen Trajektorien zu
betrachten.
- Deshalb wird im allgemeinen eine größere Klasse von stochastischen
Prozessen betrachtet, die alle praktisch relevanten Beispiele
umfasst und deren Trajektorien gleichzeitig gute
Regularitätseigenschaften besitzen.
- Dabei wird nur gefordert, dass die Trajektorien überall
rechtsstetig sind und linksseitige Grenzwerte besitzen.
Hinreichende Bedingungen hierfür sind durch das folgende Theorem
gegeben.
Theorem 1.2

Sei

ein beliebiger reellwertiger Prozess, und
sei
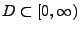
eine abzählbare Menge, die dicht in
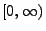
liegt. Falls
- (i)
 rechtsstetig in Wahrscheinlichkeit ist, d.h., für
beliebige
rechtsstetig in Wahrscheinlichkeit ist, d.h., für
beliebige  und
und
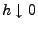 gilt
gilt
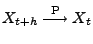 ,
wobei
,
wobei
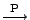 die Konvergenz in Wahrscheinlichkeit bezeichnet,
die Konvergenz in Wahrscheinlichkeit bezeichnet,
- (ii)
- die Trajektorien von
 für jedes
für jedes 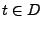 mit
Wahrscheinlichkeit
mit
Wahrscheinlichkeit  endliche rechts- und linksseitige
Grenzwerte besitzen, d.h., für jedes
endliche rechts- und linksseitige
Grenzwerte besitzen, d.h., für jedes 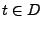 existieren die
Grenzwerte
existieren die
Grenzwerte
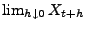 und
und
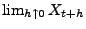 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit  ,
,
dann gibt es eine Version
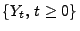
von

, so dass mit Wahrscheinlichkeit

- (a)
- die Trajektorien von
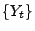 rechtsstetig sind und
rechtsstetig sind und
- (b)
- linksseitige Grenzwerte besitzen, d.h.,
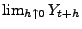 existiert für jedes
existiert für jedes  .
.
Der Beweis von Theorem 1.2 geht über den
Rahmen dieser Vorlesung hinaus und wird deshalb weggelassen; er
kann beispielsweise in Breiman (1992), S. 300 nachgelesen werden.
Theorem 1.3
(A.N. Kolmogorow)

Sei

ein beliebiger reellwertiger Prozess, so
dass es Konstanten
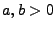
und
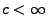
gibt mit
Dann gibt es eine stetige Modifikation von

.
Einen Beweis von Theorem 1.3 kann man zum
Beispiel in Krylov (2002), S. 20-21 nachlesen.




Nächste Seite: Modifikationen von càdlàg Prozessen
Aufwärts: Einleitung
Vorherige Seite: Endlich-dimensionale Verteilungen; Existenzsatz von
Inhalt
Ursa Pantle
2005-07-13
![]() stets existierende stochastische Prozess,
der diese Wahrscheinlichkeitsmaße als endlich-dimensionale
Verteilungen hat, im allgemeinen nicht eindeutig bestimmt
ist.
stets existierende stochastische Prozess,
der diese Wahrscheinlichkeitsmaße als endlich-dimensionale
Verteilungen hat, im allgemeinen nicht eindeutig bestimmt
ist.
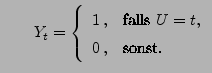
![]() , die durch Eigenschaften der
Trajektorien gegeben sind, im allgemeinen nicht messbar bezüglich
der
, die durch Eigenschaften der
Trajektorien gegeben sind, im allgemeinen nicht messbar bezüglich
der ![]() -Algebra
-Algebra
![]() sein müssen, die durch die
Zylinder-Mengen in (4) erzeugt wird.
sein müssen, die durch die
Zylinder-Mengen in (4) erzeugt wird.
![$\displaystyle A=\bigcap_{\mbox{$t\in[0,1]$, $t$\ rational}}
\{\omega\in\Omega:\,X_t(\omega)=0\}\,,
$](img92.png)