



Nächste Seite: Transformationssätze; radiale Simulation von
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Messbare Indizierung der Atome
Inhalt
Simulationsalgorithmus; Akzeptanz- und Verwerfungsmethode
Sei
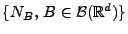 ein Poisson-Prozess mit dem
(diffusen und lokal endlichen) Intensitätsmaß
ein Poisson-Prozess mit dem
(diffusen und lokal endlichen) Intensitätsmaß 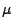 , und seien
, und seien
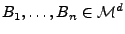 paarweise disjunkte Quader mit der in
(2) gegebenen Form, so dass
paarweise disjunkte Quader mit der in
(2) gegebenen Form, so dass
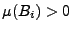 für jedes
für jedes
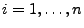 .
.
Um den Poisson-Prozess 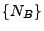 in der beschränkten
Borel-Menge
in der beschränkten
Borel-Menge
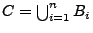 zu simulieren, genügt es zu
beachten,
zu simulieren, genügt es zu
beachten,
- dass das zufällige Zählmaß
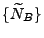 mit
mit
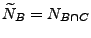 gemäß Theorem 4.10 ein
Poisson-Prozess mit dem endlichen Zählmaß
gemäß Theorem 4.10 ein
Poisson-Prozess mit dem endlichen Zählmaß
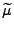 ist
wobei
ist
wobei
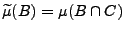 ,
,
- und dass man deshalb gemäß Theorem 4.8 bzw.
Korollar 4.2 wie folgt vorgehen kann:
- Schritt 0
 Generiere eine Realisierung von
Generiere eine Realisierung von
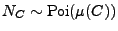 .
.
- Schritt 1
 Falls
Falls 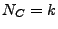 , dann generiere eine
Realisierung des multinomial verteilten Zufallsvektors
wobei
, dann generiere eine
Realisierung des multinomial verteilten Zufallsvektors
wobei
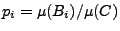 für jedes
für jedes
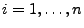 .
.
- Schritt 2
 Falls
Falls
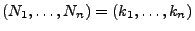 , dann generiere
, dann generiere
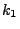 unabhängige Zufallsvektoren
unabhängige Zufallsvektoren
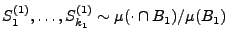 ,
,
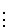
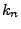 unabhängige Zufallsvektoren
unabhängige Zufallsvektoren
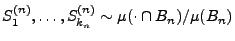 ,
,
wobei die Zufallsvektoren
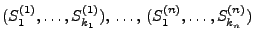 ebenfalls unabhängig sind.
ebenfalls unabhängig sind.
- Beachte
-
- Seien
 Realisierungen von
Realisierungen von
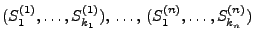 .
.
- Dann ist die (nichtgeordnete) Menge
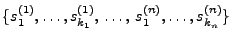 von Punkten im
von Punkten im
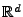 eine
Realisierung der Atome des Poisson-Prozesses
eine
Realisierung der Atome des Poisson-Prozesses 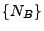 in der
Menge
in der
Menge
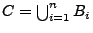 .
.
Wenn die Anzahl 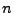 der Quader
der Quader
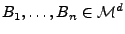 groß
ist, aus denen die Menge
groß
ist, aus denen die Menge
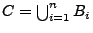 besteht, dann
kann die praktische Umsetzung der Simulationsschritte 1 und 2 mit
einem großen Rechenaufwand verbunden sein.
besteht, dann
kann die praktische Umsetzung der Simulationsschritte 1 und 2 mit
einem großen Rechenaufwand verbunden sein.
- In diesem Fall kann es effizienter sein, den Poisson-Prozess
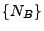 mit der folgenden Akzeptanz- und
Verwerfungsmethode in
mit der folgenden Akzeptanz- und
Verwerfungsmethode in 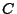 zu simulieren.
zu simulieren.
- Diese Methode hat darüber hinaus den Vorteil, dass das Gebiet
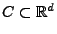 , in dem Poisson-Prozess
, in dem Poisson-Prozess 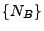 simuliert
wird, eine beliebige beschränkte Borel-Menge sein kann.
simuliert
wird, eine beliebige beschränkte Borel-Menge sein kann.
- Schritt 0
 Generiere eine Realisierung von
Generiere eine Realisierung von
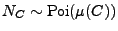 .
.
- Schritt 1
 Falls
Falls 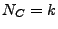 , dann generiere so lange
Realisierungen
, dann generiere so lange
Realisierungen
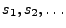 der unabhängigen Zufallsvektoren
der unabhängigen Zufallsvektoren
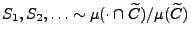 ,
bis
,
bis 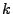 der Pseudozufallszahlen
der Pseudozufallszahlen
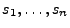 in der Menge
in der Menge 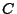 liegen, wobei
liegen, wobei
- Schritt 3
 Dann ist die (nichtgeordnete) Menge
Dann ist die (nichtgeordnete) Menge
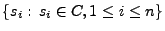 von Punkten im
von Punkten im
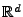 eine Realisierung der Atome des
Poisson-Prozesses
eine Realisierung der Atome des
Poisson-Prozesses 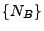 in der Menge
in der Menge 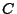 .
.




Nächste Seite: Transformationssätze; radiale Simulation von
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Messbare Indizierung der Atome
Inhalt
Ursa Pantle
2005-07-13
![]() ein Poisson-Prozess mit dem
(diffusen und lokal endlichen) Intensitätsmaß
ein Poisson-Prozess mit dem
(diffusen und lokal endlichen) Intensitätsmaß ![]() , und seien
, und seien
![]() paarweise disjunkte Quader mit der in
(2) gegebenen Form, so dass
paarweise disjunkte Quader mit der in
(2) gegebenen Form, so dass
![]() für jedes
für jedes
![]() .
.
![]() in der beschränkten
Borel-Menge
in der beschränkten
Borel-Menge
![]() zu simulieren, genügt es zu
beachten,
zu simulieren, genügt es zu
beachten,
![]() der Quader
der Quader
![]() groß
ist, aus denen die Menge
groß
ist, aus denen die Menge
![]() besteht, dann
kann die praktische Umsetzung der Simulationsschritte 1 und 2 mit
einem großen Rechenaufwand verbunden sein.
besteht, dann
kann die praktische Umsetzung der Simulationsschritte 1 und 2 mit
einem großen Rechenaufwand verbunden sein.