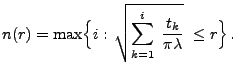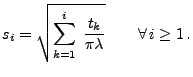Nächste Seite: Über dieses Dokument ...
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Simulationsalgorithmus; Akzeptanz- und Verwerfungsmethode
Inhalt
Transformationssätze; radiale Simulation
von homogenen Poisson-Prozessen
In diesem Abschnitt betrachten wir zwei verschiedene Arten von
Transformationen von Poisson-Prozesse im
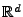 .
.
Für beliebige
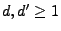 seien die Borel-Mengen
seien die Borel-Mengen
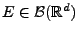 und
und
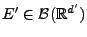 gegeben.
gegeben.
- Außerdem sei
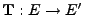 eine Borel-messbare Abbildung,
d.h., es gelte
eine Borel-messbare Abbildung,
d.h., es gelte
- wobei die Urbilder von beschränkten Borel-Mengen beschränkt
seien, d.h., es gelte
- Beachte
 Sei
Sei
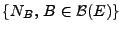 ein beliebiges Zählmaß in
ein beliebiges Zählmaß in 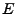 mit dem
Intensitätsmß
mit dem
Intensitätsmß
![$ \mu:\mathcal{B}(E)\to[0,\infty]$](img2339.png) . Man kann sich leicht
überlegen, dass dann durch den Ansatz
. Man kann sich leicht
überlegen, dass dann durch den Ansatz
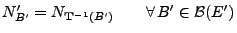 |
(15) |
ein zufälliges Zählmaß
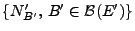 in
in 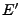 gegeben ist, wobei das
Intensitätsmaß
gegeben ist, wobei das
Intensitätsmaß
![$ \mu^\prime:\mathcal{B}(E^\prime)\to[0,\infty]$](img2343.png) von
von
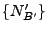 gegeben ist durch
gegeben ist durch
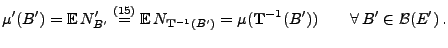 |
(16) |
Theorem 4.12
Sei
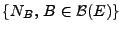
ein Poisson-Prozess in
mit dem
(diffusen und lokal endlichem) Intensitätsmaß
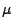
.
- Beweis
-
- Beispiele
 Sei
Sei
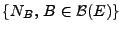 ein homogener Poisson-Prozess
in
ein homogener Poisson-Prozess
in
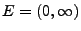 mit der Intensität
mit der Intensität 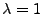 .
.
- Sei
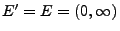 und
und
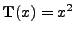 .
.
- Sei
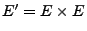 und die Abbildung
und die Abbildung
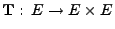 sei gegeben durch
sei gegeben durch
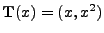 .
.
- Dann ist die Folge
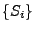 der Sprungzeitpunkte des
(Poissonschen) Zählprozesses
der Sprungzeitpunkte des
(Poissonschen) Zählprozesses
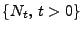 mit
mit
![$ N_t=N_{(0,t]}$](img2371.png) eine messbare Indizierung der Atome von
eine messbare Indizierung der Atome von 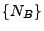 .
.
- Außerdem ist
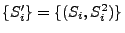 eine messbare
Indizierung der Atome eines Poisson-Prozesses
eine messbare
Indizierung der Atome eines Poisson-Prozesses
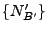 in
in
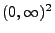 ,
,
- dessen Intensitätsmaß
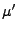 auf dem Funktionsgraphen
auf dem Funktionsgraphen
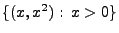 konzentriert ist.
konzentriert ist.
- Beachte: Das heißt insbesondere, dass die Atome von
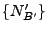 mit Wahrscheinlichkeit 1 in einer
1-dimensionalen Teilmenge von
mit Wahrscheinlichkeit 1 in einer
1-dimensionalen Teilmenge von
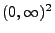 liegen.
liegen.
Wir betrachten nun noch eine andere Art der Transformation von
Poisson-Prozessen in
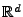 , mit deren Hilfe man
Poisson-Prozesse
, mit deren Hilfe man
Poisson-Prozesse
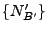 in höherdimensionalen
Räumen
in höherdimensionalen
Räumen
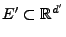 mit
mit
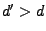 konstruieren kann, so dass der Träger des Intensitätsmaßes
konstruieren kann, so dass der Träger des Intensitätsmaßes
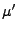 von
von
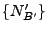 eine
eine
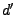 -dimensionale Menge ist.
-dimensionale Menge ist.
- Beweis
-
- Beachte
-
- Ähnlich wie bei den
zusammengesetzten Poisson-Prozessen in
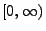 , die in Abschnitt 2.2.2
eingeführt worden sind, können die in Theorem 4.13
betrachteten Zufallsvariablen
, die in Abschnitt 2.2.2
eingeführt worden sind, können die in Theorem 4.13
betrachteten Zufallsvariablen 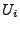 als ,,Marken'' der Atome
als ,,Marken'' der Atome
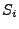 aufgefasst werden.
aufgefasst werden.
- Dabei sagt man, dass die Folge
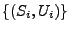 der markierten Atome eine messbare Indizierung eines unabhängig
markierten Poisson-Prozesses ist.
der markierten Atome eine messbare Indizierung eines unabhängig
markierten Poisson-Prozesses ist.
Mit Hilfe der Theoreme 4.12 und 4.13
konstruieren wir nun einen Algorithmus zur radialen
Simulation von homogenen Poisson-Prozessen im
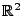 .
.
Um einen homogenen Poisson-Prozess mit der Intensität 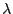 im Kreis
im Kreis
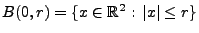 mit Radius
mit Radius 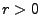 zu
simulieren, kann man also wie folgt vorgehen:
zu
simulieren, kann man also wie folgt vorgehen:
- Schritt 0
 Generiere die Pseudozufallszahlen
Generiere die Pseudozufallszahlen
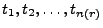 gemäß der Verteilung
gemäß der Verteilung
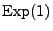 ,
wobei
,
wobei
- Schritt 1
 Generiere die Pseudozufallszahlen
Generiere die Pseudozufallszahlen
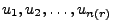 gemäß
der Verteilung
gemäß
der Verteilung
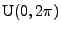 .
.
- Schritt 2
 Berechne die Pseudozufallsvektoren
Berechne die Pseudozufallsvektoren
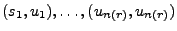 , wobei
, wobei
- Schritt 3
 Transformiere die Pseudozufallsvektoren
Transformiere die Pseudozufallsvektoren
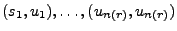 mit Hilfe der in
(19) gegebenen Abbildung
mit Hilfe der in
(19) gegebenen Abbildung
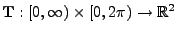 .
.
- Schritt 4
 Generiere so die Realisierung
Generiere so die Realisierung
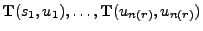 eines homogenen
Poisson-Prozesses mit der Intensität
eines homogenen
Poisson-Prozesses mit der Intensität 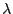 im Kreis
im Kreis
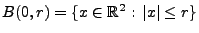 .
.




Nächste Seite: Über dieses Dokument ...
Aufwärts: Poissonsche Zählmaße im
Vorherige Seite: Simulationsalgorithmus; Akzeptanz- und Verwerfungsmethode
Inhalt
Ursa Pantle
2005-07-13
![]() .
.
![]() seien die Borel-Mengen
seien die Borel-Mengen
![]() und
und
![]() gegeben.
gegeben.
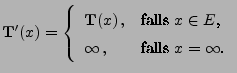
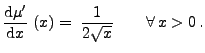
![]() , mit deren Hilfe man
Poisson-Prozesse
, mit deren Hilfe man
Poisson-Prozesse
![]() in höherdimensionalen
Räumen
in höherdimensionalen
Räumen
![]() mit
mit
![]() konstruieren kann, so dass der Träger des Intensitätsmaßes
konstruieren kann, so dass der Träger des Intensitätsmaßes
![]() von
von
![]() eine
eine
![]() -dimensionale Menge ist.
-dimensionale Menge ist.
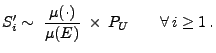
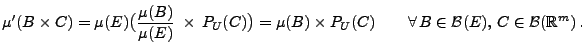
![]() .
.
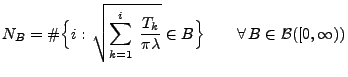
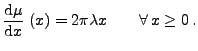
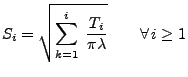
![]() im Kreis
im Kreis
![]() mit Radius
mit Radius ![]() zu
simulieren, kann man also wie folgt vorgehen:
zu
simulieren, kann man also wie folgt vorgehen: