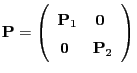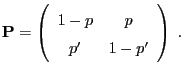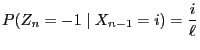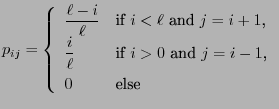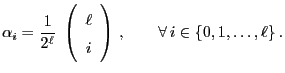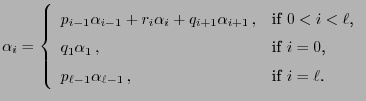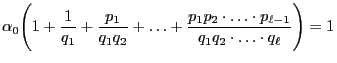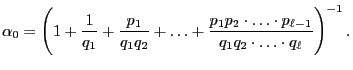Next: Stationary Initial Distributions
Up: Ergodicity and Stationarity
Previous: Estimates for the Rate
Contents
Irreducible and Aperiodic Markov Chains
- Recall
- In Theorem 2.4 we characterized the ergodicity of
the Markov chain
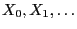 by the quasi-positivity of its
transition matrix
by the quasi-positivity of its
transition matrix
 .
.
- However, it can be difficult to show this property of
 directly, especially if
directly, especially if 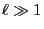 .
.
- Therefore, we will derive another (probabilistic) way to
characterize the ergodicity of a Markov chain with finite state
space. For this purpose we will need the following notion.
- For arbitrary but fixed states
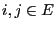 we say that the state
we say that the state
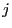 is accessible from state
is accessible from state 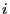 if
if
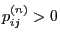 for
some
for
some 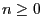 where
where
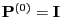 . (notation:
. (notation: 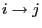 )
)
- Another (equivalent) definition for accessibility of states is the
following:
- Let
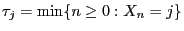 the number of steps until the
Markov chain
the number of steps until the
Markov chain 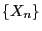 reaches the state
reaches the state 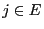 for the first
time. We define
for the first
time. We define
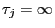 if
if 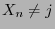 for all
for all 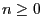 .
.
Theorem 2.7

Let
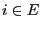
be such that
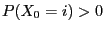
. In this case
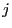
is
accessible from
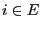
if and only if
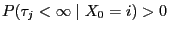
.
- Proof
-
- Remarks
-
- The property of accessibility is
- transitive, i.e.,
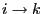 and
and 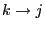 imply that
imply that 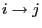 .
.
- This is an immediate consequence of the inequality
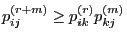 (see
Corollary 2.2) and of the definition of accessibility.
(see
Corollary 2.2) and of the definition of accessibility.
- Moreover, in case
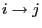 and
and 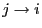 we say that the states
we say that the states
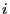 and
and 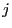 communicate. (notation:
communicate. (notation:
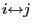 )
)
- The property of communicating is an equivalence relation as
- (a)
-
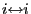 (reflexivity),
(reflexivity),
- (b)
-
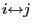 if and only if
if and only if
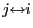 (symmetry),
(symmetry),
- (c)
-
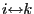 and
and
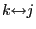 implies
implies
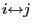 (transitivity).
(transitivity).
- As a consequence,
- the state space
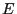 can be completely divided into disjoint
equivalence classes with respect to the equivalence relation
can be completely divided into disjoint
equivalence classes with respect to the equivalence relation
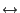 .
.
- The Markov chain
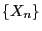 with transition matrix
with transition matrix
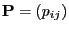 is called irreducible if the state space
is called irreducible if the state space 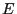 consists of only
one equivalence class, i.e.
consists of only
one equivalence class, i.e.
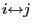 for all
for all 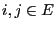 .
.
- Examples
-
- The definition of irreducibility immediately implies that the
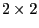 matrices
matrices
![$\displaystyle {\mathbf{P}}_1=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/2 & 1/2
\end{array}\right)$](img424.png)
and
![$\displaystyle \qquad
{\mathbf{P}}_2=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/4 & 3/4
\end{array}\right)
$](img425.png)
are irreducible.
- On the other hand the
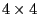 block matrix
block matrix
 consisting of
consisting of
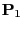 and
and
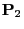 is not irreducible.
is not irreducible.
Besides irreducibility we need a second property of the transition
probabilities, namely the so-called aperiodicity, in order
to characterize the ergodicity of a Markov chain in a simple way.
- Definition
-
- The period
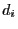 of the state
of the state 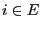 is given by
is given by
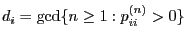 where ,,gcd'' denotes the greatest
common divisor. We define
where ,,gcd'' denotes the greatest
common divisor. We define
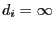 if
if
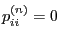 for all
for all
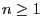 .
.
- A state
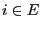 is said to be aperiodic if
is said to be aperiodic if 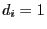 .
.
- The Markov chain
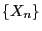 and its transition matrix
and its transition matrix
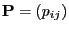 are called aperiodic if all states of
are called aperiodic if all states of
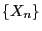 are aperiodic.
are aperiodic.
We will now show that the periods 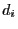 and
and 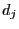 coincide if the
states
coincide if the
states 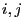 belong to the same equivalence class of communicating
states. For this purpose we introduce the notation
belong to the same equivalence class of communicating
states. For this purpose we introduce the notation ![$ i\to j[n]$](img437.png) if
if
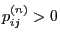 .
.
- Proof
-
- If
![$ j\to j[n]$](img439.png) ,
, ![$ i\to j[k]$](img440.png) and
and ![$ j\to i[m]$](img441.png) for certain
for certain
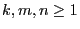 , then the inequalities from Corollary 2.2 imply that
, then the inequalities from Corollary 2.2 imply that
![$ i\to i[k+m]$](img443.png) and
and
![$ i\to i[k+m+n]$](img444.png) .
.
- Thus,
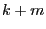 and
and 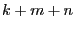 are divisible by
are divisible by 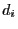 .
.
- As a consequence the difference
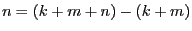 is also divisible
by
is also divisible
by 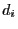 .
.
- This shows that
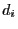 is a common divisor for all natural numbers
is a common divisor for all natural numbers
 having the property that
having the property that
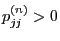 , i.e.
, i.e.
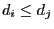 .
.
- For reasons of symmetry the same argument also proves that
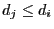 .
.

Corollary 2.5

Let the Markov chain
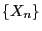
be irreducible.
Then all states of
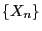
have the same period.
In order to show
- that the characterization of an ergodic Markov chain (see
Theorem 2.4) considered in Section 2.2.1
is equivalent to the Markov chain being irreducible and aperiodic,
- we need the following elementary lemma from number theory.
Lemma 2.3
Let
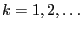
an arbitrary but fixed natural number. Then there
is a natural number
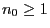
such that
- Proof
-
Theorem 2.9

The transition matrix

is quasi-positive if and only if

is irreducible and aperiodic.
- Proof
-
- Remarks
-
- Example
 (Diffusion Model)
(Diffusion Model)
see P. Brémaud (1999)
Markov Chains, Gibbs Fields, Monte Carlo Simulation, and
Queues. Springer, New York, p.76
- The following simple model describing a diffusion process through a
membrane was suggested in 1907 by the physicists Tatiana and Paul
Ehrenfest. It is designed to model the heat exchange between two
systems at different temperatures.
- The random variables
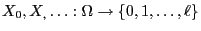 can thus be defined recursively
can thus be defined recursively
- In spite of this, the linear equation system
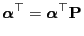 |
(56) |
has a (uniquely determined) probability solution
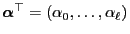 where
where
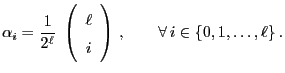 |
(57) |
- Remarks
-




Next: Stationary Initial Distributions
Up: Ergodicity and Stationarity
Previous: Estimates for the Rate
Contents
Ursa Pantle
2006-07-20
 by the quasi-positivity of its
transition matrix
by the quasi-positivity of its
transition matrix
 .
.
 directly, especially if
directly, especially if 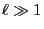 .
.
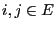 we say that the state
we say that the state
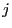 is accessible from state
is accessible from state 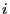 if
if
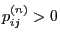 for
some
for
some 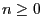 where
where
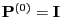 . (notation:
. (notation: 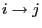 )
)
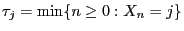 the number of steps until the
Markov chain
the number of steps until the
Markov chain 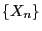 reaches the state
reaches the state 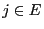 for the first
time. We define
for the first
time. We define
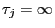 if
if 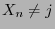 for all
for all 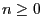 .
.
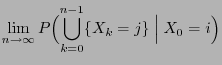
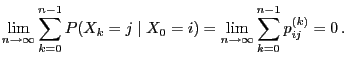
![$\displaystyle {\mathbf{P}}_1=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/2 & 1/2
\end{array}\right)$](img424.png) and
and![$\displaystyle \qquad
{\mathbf{P}}_2=\left(\begin{array}{ll}
1/2 &1/2\\ [2pt]
1/4 & 3/4
\end{array}\right)
$](img425.png)